| 100-Level | ....... | 200-Level | ....... | 300-Level | ....... | 400-Level |

100-Series Courses

 Approximating a tangent line with a convergent sequence of secants. |
An introduction to the methods and applications of calculus. Derivatives, exponential and logarithmic functions, optimization problems, related rates, integration, partial derivatives, differential equations. Selected applications from the natural and social sciences. Not available to students enrolled in or with credit for Mathematics 110. Not for credit towards a major in Mathematics.
|
|
An examination of the concepts and techniques of calculus, with applications to other areas of mathematics and the physical and social sciences.
|
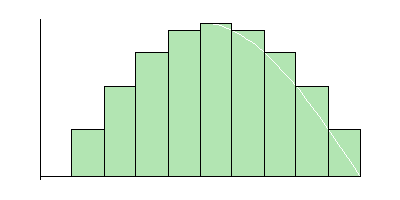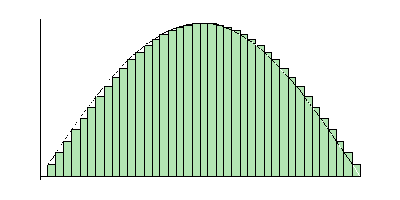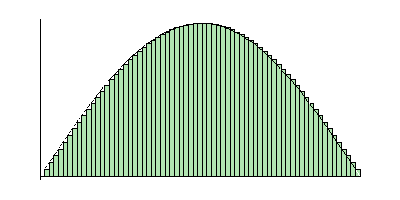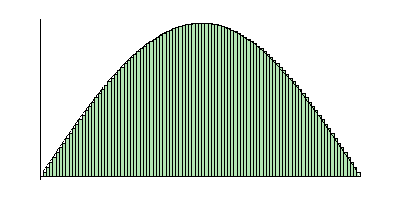 Computing an integral with a convergent sequence of Riemann sums. |
Vectors, systems of linear equations, matrices, determinants, linear transformations, eigenvalues and eigenvectors. Excludes Mathematics 130.
- Prerequisite: A Grade 12U or U/C mathematics course or OAC Mathematics credit with at least 60%.
- Meetings: Three hours lecture and one hour workshop weekly.
- Timetables:
- Instructors:
- Fall section: David Poole
- Winter section: Xiaorang Li
- For more information, please see the MATH 135H home page.
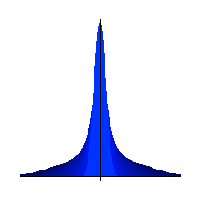 Seven Gaussian distributions of increasing variance. |
Data summary, elementary probability, estimation, hypothesis testing, comparative methods, analysis of variance, regression, nonparametric methods, introduction to elementary applications of statistical computing. This course uses highschool mathematics as a foundation and involves the use of computers.Not credited toward Mathematics major requirements, nor available to students enrolled in, or with credit for Mathematics-Statistics 251H or Mathematics 110.
|
Probability, random variables, probability distributions. Not available to students with credit for Mathematics-Statistics 251H.
- Corequisite: Mathematics 105H or Mathematics 110 taken previously or concurrently.
- Meetings: Three one-hour lectures weekly and one-hour workshop fortnightly.
- Timetables:
- Instructors:
- Fall section: Ion Rada
- Winter section: Michelle Boue.
- Oshawa section:
- For more information, please see the Fall Math 155 Homepage or Spring Math 155 Homepage or the Statistics Courses Page.

200-Series Courses

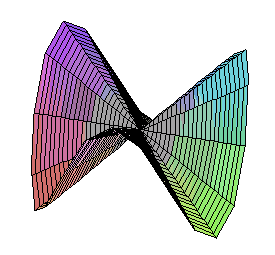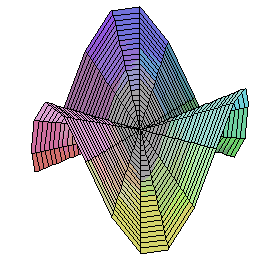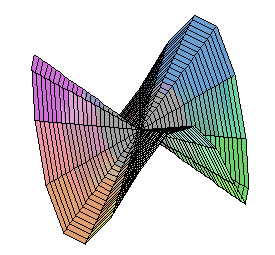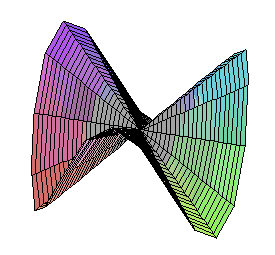 The Monkey's Saddle is not differentiable at zero, but all tangent lines exist there. |
Vector geometry, curves, surfaces in three dimensions. Partial differentiation and applications, multiple integrals. Vector calculus.
|
Synopsis:: First order equations; qualitative and numerical methods. Second order linear equations. Applications to physical and biological models. Laplace transforms. Power series solutions. |
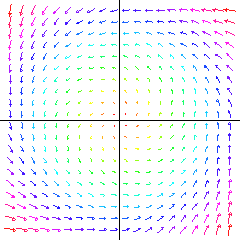 A two-dimensional vector field determines a flow in the plane. |
|
Overview: Ordinary differential equations (ODEs) model physical systems which evolve continuously in time. For example, suppose the state of the system is described by a single variable , and satisfies the equation:
Suppose the state of the system at time is given by a real vector in . Then an ODE for this system has the form:
|
ODEs are ubiquitous in applied mathematics. For example:
Given an ODE, we can ask four questions:
|
 A sequence of successively higher order Taylor polynomials converge to the sine function. |
The real number system. Limits. Continuity. Differentiability. Mean-value theorem. Convergence of sequences and series. Uniform convergence.
|
Error analysis, non-linear equations, linear systems, interpolation methods, numerical differentiation and integration and initial value problems.
- Prerequisite: Mathematics 105H or 110.
- Meetings: Three lectures and one tutorial weekly.
- For more information, please see the MATH 207 home page or the last year's MATH 207 home page.
- Class timetable
- Instructors: Kenzu Abdella
Elements of Euclidean geometry stressing links to modern mathematical methods. Geometric transformations and symmetry. Recommended for Education students.
- Prerequisite: Either Mathematics 105H or 110 (with OAC Algebra/Geometry recommended), or 135H.
- Meetings: Two lectures and one tutorial weekly.
- Class timetable
- Instructor: Reem Yassawi
Vector spaces, basis and dimension, inner product spaces, orthogonality, linear transformations, diagonalization, determinants, eigenvalues, quadratic forms, least squares, the singular value decomposition. Excludes Mathematics 130.
- Prerequisite: Mathematics 135H.
- Meetings: Three hours lecture and one hour tutorial weekly.
- Class timetable
- Instructor: David Poole
Mathematics related to computer science including propositional logic, recursive functions, combinatorics, graphs and networks, Boolean algebras. Applications to languages, analysis of algorithms, optimization problems, coding theory, and circuit design.
- Prerequisite: Mathematics 110 or 130 or 135H; or Computer Science 102H together with one Grade 12 U or U/C or OAC credit in Mathematics.
- Recommended: OAC Finite Mathematics.
- Meetings: Three hours weekly.
- Class timetable
- Instructor: Marco Pollanen
- For more information, please see the MATH 260 home page.
A course in mathematics and mathematical thinking for prospective school teachers. Number systems and counting, graphs and networks, probability and statistics, measurement and growth, symmetry, computers and mathematics. Not available to students enrolled in or with credit for any of Mathematics 110, Mathematics 135H or Mathematics-Computer Science 260 or their equivalents. Not for credit towards any major in Mathematics.
- Note: Instructor's approval required; enrolment limited.
- Meetings: Three-hour lecture/workshop weekly.
- Timetables
- Instructor:
- Section A: Wendi Morrison
- Section B: Wendi Morrison
- Section C: Wendi Morrison
- For more information, please see the (old)Math 280 home page.

300-Series Courses

Synopsis: We'll focus on the following topics:
|
 The Wave Equation: A vibrational mode of a circular membrane. |
|
Overview: Partial differential equations (PDEs) model physical systems which
evolve continuously in time, and whose physical state is described by
some continuous function in space. For example, suppose we pour some
ink into a flat tray of water. Let
|
PDEs are ubiquitous in applied mathematics. For example:
Given a PDE we can ask four questions:
|
 Colour-coding the complex plane in polar coordinates |
Functions of a complex variable, analytic functions, complex integrals, Cauchy integral theorems, Taylor series, Laurent series, residue calculus.
|
 The complex exponential map, seen through this colour-coding. |
Differential equations in applied mathematics, including Bessel, Legendre, hypergeometric, Laguerre, Hermite, Chebyshev, etc. Series and numerical solutions. Properties of the special functions arising from these equations.
- Prerequisite: Mathematics-Physics 205H.
- Meetings: Three lectures and one tutorial weekly.
- Instructor: Not offered
- For more information, please see the MATH 308 home page.
|
Limits and continuity. Completeness, compactness, the Heine-Borel theorem. Connectedness.
|
The Chinese Box Theorem says: if |
Applied mathematics as found in the classical mechanics of particles, rigid bodies and continuous media. Motion of rigid bodies, Lagrangian mechanics, Hamiltonian mechanics, dynamics of oscillating systems.
- Prerequisites: Mathematics 200 and 205H and Mathematics-Physics 312H.
- Meetings: Three class meetings weekly.
- Class timetable
- Taught by the Department of Physics.
Applied mathematics as found in the classical mechanics of particles. One-dimensional motion, vector differential operators, three-dimensional motion, moving and rotating coordinate systems, central forces, systems of particles.
- Prerequisites: Mathematics 110 and Physics 100 or permission of the instructor.
- Pre or co-orequisite: Mathematics 200.
- Meetings: Three lectures and tutorial weekly.
- Class timetable
- Taught by the Department of Physics.
Overview: Number theory is one of the oldest and richest areas of mathematics, and ubiquitous in contemporary mathematical research. We will likely examine the following topics: Prime Numbers: The Fundamental Theorem of Arithmetic says every number has a unique factorization into primes. We'll prove this theorem, and study its consequences.
Diophantine Equations: A Pythagorean triple is a triple
of integers |
The Lattice of Divisibility of integers. The equation Fermat's famous Last Theorem says this equation
has no nontrivial solutions for Modular arithmetic is the arithmetic of 12 hour clocks, 7 day weeks, etc., and is fundamental to the theory of groups and rings. We will develop the basic theory of congruence relations. We will then look into congruence equations, focusing on such topics as:
| |
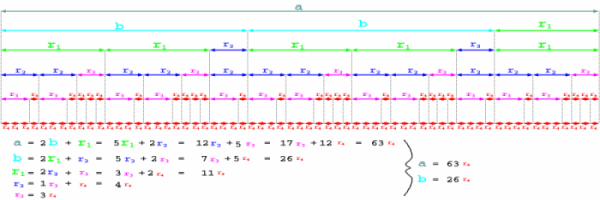
The Euclidean algorithm is a method to compute the greatest common divisor of two numbers. | ||
|
Elements of projective and non-Euclidean geometries, including an introduction to axiomatic systems.
|
Overview: We will study three kinds of algebraic structures: groups, rings, and fields. Group Theory: Groups encode the symmetries other objects. For example:
Groups can also be thought of as `abstract spaces', or used to encode geometric/topological information. For example
Ring Theory: Rings are algebraic structures which encode abstract arithmetic.
Field Theory: A field is a special kind of ring with a particularly rich algebraic structure. The rational numbers, the real numbers, and the complex numbers are examples of fields. Field theory reveals important limitations to mathematical methods. For example:
|
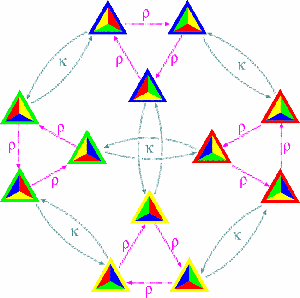
The group of symmetries of a tetrahedron 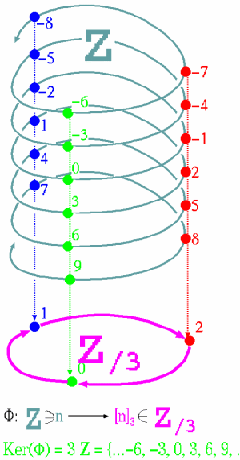
A group epimorphism from |
Introduction to the concepts, techniques and applications of linear programming and discrete optimization. Topics include the simplex method, dynamic programming, duality, game theory, transportation problems, assignment problems, matchings in graphs, network flow theory, and combinatorial optimization with emphasis on integer programming.
- Prerequisites: Mathematics 130 or 135H, and Mathematics-Computer Science 260.
- Meetings: Two lectures and one tutorial weekly.
- Class timetable
- Instructor: Marco Pollanen
- For more information, please see the MATH 341 home page.
Introduction to mathematical statistics: exploring and describing relationships, sampling, point and interval estimation, likelihood methods, hypothesis testing, comparative inferences, contingency tables, linear regression and correlation introductory multiple regression, design and analysis of experiments, nonparametric methods. Assumes a background in probability and uses introductory linear algebra. Excludes Mathematics-Statistics 252H.
- Prerequisites: Mathematics-Statistic 155H, Mathematics 105H or 110.
- Strongly recommended: Mathematics 135H
- Meetings: Three lectures weekly and one hour workshop occasionally.
- Class timetable
- Instructor: Michelle Boue
- For more information, please see the Math 355 Homepage or the Statistics Courses Page.
A study of the major currents of mathematical thought from ancient to modern times.
- Prerequisites: Mathematics 110 and 235H, or Mathematics 110 and permission of the instructor. Second-year students wishing to take the course must have permission of the instructor.
- Meetings: Three hours weekly.
- Instructor: Not offered
- For more information, please see the MATH 380 home page.

400-Series Courses

Riemann and Lebesque measure, integration.
- Prerequisites: Mathematics 206H, 310H.
- Meetings: Three hours weekly.
- Instructor: Not offered
 The Riemann surface of the complex cube root function. |
|
Differential equations, ordinary and partial.
- Prerequisite: Mathematics-Physics 305H.
- Meetings: Three hours weekly.
- Class timetable
- Instructor: Kenzu Abdella
- For more information, please see the MATH 411 home page.
|
An introduction to the syntax and semantics of propositional and first-order logics through the Soundness, Completeness and Compactness Theorems.
|
An introduction to computability via Turing machines and recursive functions, followed either by applications to the Incompleteness Theorem or by an introduction to complexity theory.
- Prerequisite: Computer Science 305H or Mathematics 330 or Mathematics-Computer Science 415H or permission of the instructor.
- Instructor: Not offered
- Prerequisite: Mathematics 225 or 226H or 326H.
- Meetings: To be arranged
- Instructor: Not offered
Extension fields and Galois groups.
- Prerequisite: Mathematics 330.
- Meetings: To be arranged.
- Instructor: David Poole
- Prerequisite: Mathematics 330.
- Meetings: To be arranged
- Instructor: Not offered
- Prerequisite: Mathematics 310H
- Meetings: To be arranged
- Instructor: Not offered
- Prerequisite: Mathematics 310H.
- Meetings: To be arranged
- Instructor: Not offered
- Prerequisites: Mathematics 355.
- Meetings: To be arranged
- Instructor: Not offered
- For more information, please see the Statistics Courses Page.
- Prerequisite: Mathematics 355.
- Meetings: To be arranged
- Instructor: Not offered
- For more information, please see the Statistics Courses Page.
- Prerequisite: Mathematics-Computer Science 260 or permission ofthe instructor.
- Recommended: Mathematics 330.
- Meetings: Three hours weekly.
- Instructor: Not offered
- For more information, please see the MA 460 home page.
|
 The Julia set for |
A survey of current research areas in mathematics, with two-week introductions to a variety of topics.
- Prerequisites: Mathematics 200, Math 235, and one 300-level mathematics course.
- Instructor: Several faculty members will participate
- Prerequisite: Permission of the instructor.
- Meetings: To be arranged.
- Instructor:
