ANSWERS TO KNOT VII.
Problem.---Given that one glass of lemonade, 3 sandwiches, and 7 biscuits, cost 1s. 2d.}; and that one glass of lemonade, 4 sandwiches, and 10 biscuits, cost 1s. 5d.: find the cost of (1) a glass of lemonade, a sandwich, and a biscuit; and (2) 2 glasses of lemonade, 3 sandwiches, and 5 biscuits.*
Answer.---(1) 8d.; (2) 1s. 7d.
* A note for American readers: Knot VII. In British currency, a shilling contains twelve pence. The phrase "One and two-pence" (written 1 s. 2 d.) means "one shilling and two-pence."
Solution.---This is best treated algebraically. Let x= the cost (in pence) of a glass of lemonade, y of a sandwich, and z of a biscuit. Then we have x + 3y + 7z = 14, and x + 4y + 10z = 17. And we require the values of x + y + z and of 2x + 3y + 5z. Now, from two equations only, we cannot find, separately, the values of three unknowns: certain combinations of them may. however, be found. Also we know that we can, by the help of the given equations, eliminate 2 of the 3 unknowns from the quantity whose value is required, which will then contain one only. If, then, the required value is ascertainable at all, it can only be by the 3rd unknown vanishing of itself: otherwise the problem is impossible.
Let us then eliminate lemonade and sandwiches, and reduce everything to biscuits---a state of things even more depressing than "if all the world were apple-pie"---by subtracting the 1st equation from the 2nd, which eliminates lemonade, and gives y+3z = 3, or y = 3-3z; and then substituting this value of y in the 1st, which gives x-2z = 5, i.e. x = 5+2z. Now if we substitute these values of x, y, in the quantities whose values are required, the first becomes (5+2z) + (3-3z) + z, i.e. 8: and the second becomes 2(5+2z) + 3(3-3z) + 5z, i.e. 19. Hence the answers are (1) 8d., (2) 1s. 7d.
The above is a universal method: that is, it is absolutely certain either to produce an answer, or to prove that no answer is possible. The question may also be solved by combining the quantities whose values are given, so as to form those whose values are required. This is merely a matter of ingenuity and good luck: and as it may fail, even when the thing is possible, ans is of no use in proving it impossible, I cannot rank this method as equal in value with the other. Even when it succeeds, it may prove a very tedious process. Suppose the 26 competitors, who have sent in what I may call accidental solutions, had had a question to deal with where every number contained 8 or 10 digits! I suspect it would have been a case of "silvered is the raven hair" (see "Patience") before any solution would have been hit on by the most ingenious of them.
Forty-five answers have come in, of which 44 give, I am happy to say, some sort of working, and therefore deserve to be mentioned by name, and to have their virtues, or vices as the case may be, discussed. Thirteen have made assumptions to which they have no right, and so cannot figure in the Class-list, even though, in 10 of the 12 cases, the answer is right. Of the remaining 28, no less than 26 have sent in accidental solutions, and therefore fall short of the highest honours.
I will now discuss individual cases, taking the worst first, as my custom is.
FROGGY gives no working---at least this is all he gives: after stating the given equations, he says "therefore the difference, 1 sandwich + 3 biscuits, = 3d.": then follow the amounts of the unknown bills, with no further hint as to how he got them. FROGGY has had a very narrow escape of not being named at all!
Of those who are wrong, VIS INERTIAE has sent in a piece of incorrect working. Peruse the horrid details, and shudder! She takes x (call it "y") as the cost of a sandwich, and concludes (rightly enough) that a biscuit will cost (3-y)/3. She then subtracts the second equation from the first, and deduces 3y + 7  (3-y)/3 - 4y + 1-
(3-y)/3 - 4y + 1-  (3-y)/3 = 3. By making two mistakes in this line, she brings out y = 3/2. Try it again, oh VIS INERTIAE! Away with INERTIAE: infuse a little more VIS: and you will bring out the correct (though uninteresting) result, 0 = 0! This will show you that it is hopeless to try to coax any one of these 3 unknowns to reveal its separate value. The other competitor, who is wrong throughout, is either J. M. C. or T. M. C.: but, whether he be a Juvenile Mis-Calculator or a True Mathematician Confused, he makes the answers 7d. and 1s. 5d. He assumes, with Too Much Confidence, that biscuits were
(3-y)/3 = 3. By making two mistakes in this line, she brings out y = 3/2. Try it again, oh VIS INERTIAE! Away with INERTIAE: infuse a little more VIS: and you will bring out the correct (though uninteresting) result, 0 = 0! This will show you that it is hopeless to try to coax any one of these 3 unknowns to reveal its separate value. The other competitor, who is wrong throughout, is either J. M. C. or T. M. C.: but, whether he be a Juvenile Mis-Calculator or a True Mathematician Confused, he makes the answers 7d. and 1s. 5d. He assumes, with Too Much Confidence, that biscuits were  d. each, and that Clara paid for 8, though she only ate 7!
d. each, and that Clara paid for 8, though she only ate 7!
We will now consider the 13 whose working is wrong, though the answer is right: and, not to measure their demerits too exactly, I will take them in alphabetical order. ANITA finds (rightly) that "1 sandwich and 3 biscuits cost 3d.," and proceeds "therefore 1 sandwich = 1 d., 3 biscuits = 1
d., 3 biscuits = 1 d., 1 lemonade = 6d." DINAH MITE begins like ANITA: and thence proves (rightly) that a biscuit costs less than a 1d.: whence she concludes (wrongly) that it must cost
d., 1 lemonade = 6d." DINAH MITE begins like ANITA: and thence proves (rightly) that a biscuit costs less than a 1d.: whence she concludes (wrongly) that it must cost  d. F. C. W. is so beautifully resigned to the certainty of a verdict of "guilty," that I have hardly the heart to utter the word, without adding a "recommended to mercy owing to extenuating circumstances." But really, you know, where are the extenuating circumstances? She begins by assuming that lemonade is 4d. a glass, and sandwiches 3d. each, (making with the 2 given equations, four conditions to be fulfilled by three miserable unknowns!). And, having (naturally) developed this into a contradiction, she then tries 5d. and 2d. with a similar result. (N.B. This process might have been carried on through the whole of the Tertiary Period, without gratifying one single Megatherium.) She then, by a "happy thought," tries half-penny biscuits, and so obtains a consistent result. This may be a good solution, viewing the problem as a conundrum: but it is not scientific. JANET identifies sandwiches with biscuits! "One sandwich + 3 biscuits" she makes equal to "4." Four what? MAYFAIR makes the astounding assertion that the equation, s + 3b = 3, "is evidently only satisfied by s = 3/2, b =
d. F. C. W. is so beautifully resigned to the certainty of a verdict of "guilty," that I have hardly the heart to utter the word, without adding a "recommended to mercy owing to extenuating circumstances." But really, you know, where are the extenuating circumstances? She begins by assuming that lemonade is 4d. a glass, and sandwiches 3d. each, (making with the 2 given equations, four conditions to be fulfilled by three miserable unknowns!). And, having (naturally) developed this into a contradiction, she then tries 5d. and 2d. with a similar result. (N.B. This process might have been carried on through the whole of the Tertiary Period, without gratifying one single Megatherium.) She then, by a "happy thought," tries half-penny biscuits, and so obtains a consistent result. This may be a good solution, viewing the problem as a conundrum: but it is not scientific. JANET identifies sandwiches with biscuits! "One sandwich + 3 biscuits" she makes equal to "4." Four what? MAYFAIR makes the astounding assertion that the equation, s + 3b = 3, "is evidently only satisfied by s = 3/2, b =  "! OLD CAT believes that the assumption that a sandwich costs 1
"! OLD CAT believes that the assumption that a sandwich costs 1 d. is "the only way to avoid unmanageable fractions." But why avoid them? Is there not a certain glow in taming such a fraction? "Ladies and gentlemen, the fraction now before you is one that defied all efforts of a refining nature: it was, in a word, hopelessly vulgar. Treating it as a circulating decimal (the treadmill of fractions) only made it worse. As a last resort, I reduced it to its lowest terms, and extracted its square root!" Joking apart, let me thank OLD CAT for some very kind words of sympathy, in reference to a correspondent (whose name I am happy to say I have now forgotten) who had found fault with me as a discourteous critic. O. V. L. is beyond my comprehension. He tales the given equations as (1) and (2): thence, by the process [(1) - (2)] deduces (rightly) equation (3) viz. s + 3b = 3: and thence again, by the process [
d. is "the only way to avoid unmanageable fractions." But why avoid them? Is there not a certain glow in taming such a fraction? "Ladies and gentlemen, the fraction now before you is one that defied all efforts of a refining nature: it was, in a word, hopelessly vulgar. Treating it as a circulating decimal (the treadmill of fractions) only made it worse. As a last resort, I reduced it to its lowest terms, and extracted its square root!" Joking apart, let me thank OLD CAT for some very kind words of sympathy, in reference to a correspondent (whose name I am happy to say I have now forgotten) who had found fault with me as a discourteous critic. O. V. L. is beyond my comprehension. He tales the given equations as (1) and (2): thence, by the process [(1) - (2)] deduces (rightly) equation (3) viz. s + 3b = 3: and thence again, by the process [ 3] (a hopeless mystery), deduces 3s + 4b = 4. I have nothing to say about it: I give it up. SEA-BREEZE says "it is immaterial to the answer" (why?) "in what proportion 3d. is divided between the sandwich and the 3 biscuits": so she assumes s = 1
3] (a hopeless mystery), deduces 3s + 4b = 4. I have nothing to say about it: I give it up. SEA-BREEZE says "it is immaterial to the answer" (why?) "in what proportion 3d. is divided between the sandwich and the 3 biscuits": so she assumes s = 1 d., b =
d., b =  d. STANZA is one of very irregular metre. At first she (like JANET) identifies sandwiches with biscuits. She then tries two assumptions (s = 1, b =
d. STANZA is one of very irregular metre. At first she (like JANET) identifies sandwiches with biscuits. She then tries two assumptions (s = 1, b =  , and s =
, and s =  , b = 5/6), and (naturally) ends in contradictions. Then she returns to the first assumption, and finds the 3 unknowns separately: quod est absurdum. STILETTO identifies sandwiches and biscuits as "articles." Is the word ever used by confectioners? I fancied "What is the next article, Ma'am?" was limited to linendrapers. TWO SISTERS first assume that biscuits are 4 a penny, and then that they are 2 a penny, adding that "the answer will of course be the same in both cases." It is a dreamy remark, making one feel something like Macbeth grasping at the spectral dagger. "Is this a statement that I see before me?" If you were to say "we both walked the same way this morning," and I were to say "one of you walked the same way, but the other didn't," which of the three would be the most hopelessly confused? TURTLE PYATE (what is a Turtle Pyate, please?) and OLD CROW, who send a joint answer, and Y. Y., adopt the same method. Y. Y. gets the equation s + 3b = 3: and then says "this sum must be apportioned in one of the three following ways." It may be, I grant you: but Y. Y. do you say "must"? I fear it is possible for Y. Y. to be two Y's. The other two conspirators are less positive: they say it "can" be so divided: but they add "either of the three prices being right"! This is bad grammar and bad arithmetic at once, oh mysterious birds!
, b = 5/6), and (naturally) ends in contradictions. Then she returns to the first assumption, and finds the 3 unknowns separately: quod est absurdum. STILETTO identifies sandwiches and biscuits as "articles." Is the word ever used by confectioners? I fancied "What is the next article, Ma'am?" was limited to linendrapers. TWO SISTERS first assume that biscuits are 4 a penny, and then that they are 2 a penny, adding that "the answer will of course be the same in both cases." It is a dreamy remark, making one feel something like Macbeth grasping at the spectral dagger. "Is this a statement that I see before me?" If you were to say "we both walked the same way this morning," and I were to say "one of you walked the same way, but the other didn't," which of the three would be the most hopelessly confused? TURTLE PYATE (what is a Turtle Pyate, please?) and OLD CROW, who send a joint answer, and Y. Y., adopt the same method. Y. Y. gets the equation s + 3b = 3: and then says "this sum must be apportioned in one of the three following ways." It may be, I grant you: but Y. Y. do you say "must"? I fear it is possible for Y. Y. to be two Y's. The other two conspirators are less positive: they say it "can" be so divided: but they add "either of the three prices being right"! This is bad grammar and bad arithmetic at once, oh mysterious birds!
Of those who win honours, THE SHETLAND SNARK must have the 3rd class all to himself. He has only answered half the question, viz. the amount of Clara's luncheon: the two little old ladies he pitilessly leaves in the midst of their "difficulty." I beg to assure him (with thanks for his friendly remarks) that entrance-fees and subscriptions are things unknown in that most economical of clubs, "The Knot-Untiers."
The authors of the 26 "accidental" solutions differ only in the number of steps they have taken between the data and the answers. In order to do them full justice I have arranged the 2nd class in sections, according to the number of steps. The two Kings are fearfully deliberate! I suppose walking quick, or taking short cuts, is inconsistent with kingly dignity: but really, in reading THESEUS' solution, one almost fancied he was "marking time," and making no advance at all! The other King will, I hope, pardon me for having altered "Coal" into "Cole." King Coilus, or Coil, seems to have reigned soon after Arthur's time. Henry of Huntington identifies him with the King Coël who first built walls round Colchester, which was named after him. In the Chronicle of Robert of Gloucester we read:---
"Aftur King Aruirag, of wam we habbeth y told,
Marius ys sone was kyng, quoynte mon & bold.
And ys sone was aftur hym, Coil was ys name,
Bothe it were quoynte men, & of noble fame."
BALBUS lays it down as a general principle that "in order to ascertain the cost of any one luncheon, it must come to the same amount upon two different assumptions." (Query. Should not "it" be "we"? Otherwise the luncheon is represented as wishing to ascertain its own cost!) He then makes two assumptions---one, that sandwiches cost nothing; the other, that biscuits cost nothing, (either arrangement would lead to the shop being inconveniently crowded!)---and brings out the unknown luncheons as 8d. and 19d., on each assumption. He the concludes that this agreement of results "shows that the answers are correct." Now I propose to disprove his general law by simply giving one instance of its failing. One instance is quite enough. In logical language, in order to disprove a "universal affirmative," it is enough to prove its contradictory, which is a "particular negative." (I must pause for a digression on Logic, and especially on Ladies' Logic. The universal affirmative "everybody says he's a duck" is crushed instantly by proving the particular negative "Peter says he's a goose," which is equivalent to "Peter does not say he's a duck." And the universal negative "nobody calls on her" is well met by the particular affirmative "I called yesterday." In short, either of two contradictories disproves the other: and the moral is that, since a particular proposition is much more easily proved than a universal one, it is the wisest course, in arguing with a Lady, to limit one's own assertions to "particulars,”: and leave her to prove the "universal" contradictory, if she can. You will thus generally secure a logical victory: a practical victory is not to be hoped for, since she can always fall back upon the crushing remark "that has nothing to do with it!"---a move for which Man has not yet discovered any satisfactory answer. Now let us return to BALBUS.) Here is my "particular negative," on which to test his rule. Suppose the to recorded luncheons to have been "2 buns, one queen-cake, 2 sauasage-rolls, and a bottle of Zoëdone: total, one-and-ninepence," and "one bun, 2 queen-cakes, a sausage-roll, and a bottle of Zoëdone: total, one-and-fourpence." And suppose Clara's unknown luncheon to have been "3 buns, one queen-cake, one sausage-roll, and 2 bottles of Zoëdone:" while the two little sisters had been indulging in "8 buns, 4 queen-cakes, 2 sausage-rolls, and 6 bottles of Zoëdone." (Poor souls, how thirsty they must have been!) If BALBUS will kindly try this by his principle of "two assumptions," first assuming that a bun is 1d. and a queen-cake 2d., and then that a bun is 3d. and a queen-cake 3d., he will bring out the other two luncheons, on each assumption, as "one-and-ninepence" and "four-and-ten-pence" respectively, which harmony of results, he will say, "shows that the answers are correct." And yet, as a matter of fact, the buns were 2d. each, the queen-cakes 3d., the sausage-rolls 6d., and the Zoëdone 2d. a bottle: so that Clara's third luncheon had cost one-and-sevenpence, and her thirsty friends had spent four-and-fourpence!
Another remark of BALBUS I will quote and discuss: for I think that it also may yield a moral for some of my readers. He says "it is the same thing in substance whether in solving this problem we use words and call it Arithmetic, or use letters and signs and call it Algebra." Now this does not appear to me a correct description of the two methods: the Arithmetical method is that of "synthesis" only; it goes from one known fact to another, until it reaches its goal: whereas the Algebraical method is that of "analysis:" it begins with the goal, symbolically represented, and so goes backwards, dragging its veiled victim with it, till it has reached the full daylight of known facts, in which it can tear off the veil and say "I know you!"
Take an illustration. Your house has been broken into and robbed, and you appeal to the policeman who was on duty that night. "Well, Mum, I did see a chap getting out over your garden-wall: but I was a good bit off, so I didn't chase him, like. I just cut down the short way to the Chequers, and who should I meet but Bill Sykes, coming full split round the corner. So I just ups and says `My lad, you're wanted.' That's all I says. And he says `I'll go along quiet, Bobby,' he says, `without the darbies,' he says." There's your Arithmetical policeman. Now try the other method. "I seed somebody a running, but he was well gone or ever I got nigh the place. So I just took a look round in the garden. And I noticed the foot-marks, where the chap had come right across your flower-beds. They was good big foot marks sure-ly. And I noticed as the left foot went down at the heel, ever so much deeper than the other. And I says to myself `The chap's been a big hulking chap: and he goes lame on his left foot.' And I rubs my hand on the wall where he got over, and there was soot on it, no mistake. So I says to myself `Now where can I light on a big man, in the chimbley-sweep line, what's lame of one foot?' And I flashes up permiscuous: and I says `It's Bill Sykes!' says I." There is your Algebraical policeman---a higher intellectual type, to my thinking, than the other.
LITTLE JACK'S solution calls for a word of praise, as he has written out what is really an algebraical proof in words, without representing any of his facts as equations. If it is all his own, he will make a good algebraist in the time to come. I beg to thank SIMPLE SUSAN for some kind words of sympathy, to the same effect as those received from OLD CAT.
HECLA and MARTREB are the only two who have used a method certain either to produce the answer, or else to prove it impossible: so they must share between them the highest honours,
CLASS LIST.
I.
| HECLA. |
 |
MARTREB. |
II.
| § 1 (2 steps). |
 |
§ 2 (3 steps). |
| ADELAIDE. |
 |
A. A. |
| CLIFTON C. . . . . |
 |
A CHRISTMAS CAROL. |
| E. K. C. |
 |
AFTERNOON TEA. |
| GUY. |
 |
AN APPRECIATIVE SCHOOLMA'AM. |
| L'INCONNU. |
 |
BABY. |
| LITTLE JACK. |
 |
BALBUS |
| NIL DESPERANDUM. |
 |
BOG-OAK. |
| SIMPLE SUSAN. |
 |
THE RED QUEEN. |
| YELLOW-HAMMER. |
 |
WALL-FLOWER |
| WOOLLY ONE. |
 |
§ 5 (6 steps). |
| § 3 (4 steps). |
 |
BAY LAUREL. |
| HAWTHORN. |
 |
BRADSHAW OF THE FUTURE. |
| JORAM. |
 |
§ 6 (9 steps). |
| S. S. G. |
 |
OLD KING COLE. |
| § 4 (5 steps). |
 |
§ 7 (14 steps). |
| A STEPNEY COACH. |
 |
THESEUS. |
III.
ANSWERS TO CORRESPONDENTS.
I HAVE received several letters on the subjects of Knots II. and VI., which lead me to think some further explanation desirable.
In Knot II., I had intended the numbering of the houses to begin at one corner of the Square, and this was assumed by most, if not all, of the competitors. TROJANUS however says "assuming, in default of any information, that the street enters the square in the middle of each side, it may be supposed that the numbering begins at a street." But surely the other is the more natural assumption?
In Knot VI., the first Problem was of course a mere jeu de mots, whose presence I thought excusable in a series of Problems whose aim is to entertain rather than to instruct: but it has not escaped the contemptuous crticisms of two of my correspondents, who seem to think that Apollo is in duty bound to keep his bow always on the stretch. Neither of them has guessed it: and this is true human nature. Only the other day---the 31st of September, to be quite exact---I met my old friend Brown, and gave him a riddle I had just heard. With one great effort of his colossal mind, Brown guessed it. "Right!" said I. "Ah," said he, "it's very neat---very neat. And it isn't an answer that would occur to everybody. Very neat indeed." A few yards further on, I fell in with Smith and to him propounded the same riddle. He frowned over it for a minute, and then gave it up. Meekly I faltered out the answer. "A poor thing, sir!" Smith growled, as he turned away. "A very poor thing! I wonder you care to repeat such rubbish!" Yet Smith's mind is, if possible, even more colossal than Brown's.
The second Problem of Knot VI. is an example in ordinary Double Rule of Three, whose essential feature is that the result depends on the variation of several elements, which are so related to it that, if all but one be constant, it varies as that one: hence, if none be constant, it varies as their product. Thus, for eaxample, the cubical contents of a rectangular tank vary as its length, if breadth and depth be constant, and so on; hence, if none be constant, it varies as the product of the length, breadth, and depth.
When the result is not thus connected with the varying elements, the Problem ceases to be Double Rule of Three and often becomes one of great complexity.
To illustrate this, let us take two candidates for a prize, A and B, who are to compete in French, German, and Italian:
(a) Let it be laid down that the result is to depend on their relative knowledge of each subject, so that, whether their marks, for French, be "1, 2" or "100, 200," the result will be the same: and let it also be laid down that if they get equal marks on 2 papers, the final marks are to have the same ratio as those of the 3rd paper. This is a case of ordinary Double Rule of Three. We multiply A's marks together, and do the same for B. Note that, if A gets a single "0," his final mark is "0," even if he gets full marks for 2 papers while B gets only one mark for each paper. This of course would be very unfair on A, though a correct solution under the given conditions.
(b) The result is to depend, as before, on relative knowledge; but French is to have twice as much weight as German or Italian. This is an unusual form of question. I should be inclined to say "the resulting ration is to nearer to the French ratio than if we multiplied as in (a), and so much nearer that it would be necessary to use the other multipliers twice to produce the same result as in (a):" e.g. if the French Ratio were 9/10, and the others 4/9, 1/9 so that the ultimate ratio, by method (a), would be 2/45, I should multiply instead by 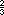 ,
, 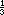 , giving the result,
, giving the result,  which is nearer to 9/10 than if he had used method (a).
which is nearer to 9/10 than if he had used method (a).
(c) The result is to depend on actual amount of knowledge of the 3 subjects collectively. Here we have to ask two questions. (1) What is to be the "unit" (i.e. "standard to measure by") in each subject? (2) Are these units to be of equal, or unequal value? The usual "unit" is the knowledge shown by answering the whole paper correctly; calling this "100," all lower amounts are represented by numbers between "0" and "100." Then, if these units are to be of equal value, we simply add A's 3 marks together, and do the same for B.
(d) The conditions are the same as (c), but French is to have double weight. Here we simply double the French marks, and add as before.
(e) French is to have such weight, that, if other marks be equal, the ultimate ratio is to be that of the French paper, so that a "0" in this would swamp the candidate: but the other two subjects are only to affect the result collectively, by the amount of knowledge shown, the two being reckoned of equal value. Here I should add A's German and Italian marks together, and multiply by his French mark.
But I need not go on: the problem may evidently be set with many varying conditions, each requiring its own method of solution. The Problem in Knot VI. was meant to belong to variety (a), and to make this clear, I inserted the following passage:
"Usually the competitors differ in one point only. Thus, last year, Fifi and Gogo made the same number of scarves in the trial week, and they were equally light; but Fifi's were twice as warm as Gogo's and she was pronounced twice as good."
What I have said will suffice, I hope, as an answer to BALBUS, who holds that (a) and (c) are the only possible varieties of the problem, and that to say "We cannot use addition, therefore we must be intended to use multiplication," is "no more illogical than, from knowledge one was not born in the night, to infer that he was born in the daytime"; and also to FIFEE, who says "I think a little more consideration will show you that our `error of adding the proportional numbers together for each candidate instead of multiplying' is no error at all." Why, even if addition had been the right method to use, not one of the writers (I speak from memory) showed any consciousness of the necessity of fixing a "unit" for each subject. "No error at all!" They were positively steeped in error!
One correspondent (I do not name him, as the communication is not quite friendly in tone) writes thus:---"I wish to add, very respectfully, that I think it would be in better taste if you were to abstain from the very trenchant expressions which you are accustomed to indulge in when criticising the answer. That such a tone must not be" ("be not"?) "agreeable to the persons concerned who have made mistakes may possibly have no great weight with you, but I hope you will feel that it would be as well not to emply it, unless you are quite certain of being correct yourself." The only instances the writer gives of the "trenchant expressions" are "hapless" and "malefactors." I beg to assure him (and any others who may need the assurance: I trust there are none) that all such words have been used in jest, and with no idea that they could possibly annoy any one, and that I sincerely regret any annoyance I may have thus inadvertently given. May I hope that in future they will recognise the distinction between severe language used in sober earnest, and the "words of unmeant bitterness,” which Coleridge has alluded to in that lovely passage beginning "A little child, a limber elf"? If the writer will refer to that passage, or to the preface to "Fire, Famine, and Slaughter," he will find the distinction, for which I plead, far better drawn out than I could hope to do in any words of mine.
The writer's insinuation that I care not how much annoyance I give to my readers I think it best to pass over in silence; but to his concluding remark I must entirely demur. I hold that to use language likely to annoy any of my correspondents would not be in the least justified by the plea that I was "quite certain of being correct." I trust that the knot-untiers and I are not on such terms as those!
I beg to thank G. B. for the offer of a puzzle---which, however, is too like the old one "Make four 9's into 100."
Stefan Bilaniuk,
Department of Mathematics,
Trent University
Maintained by Stefan Bilaniuk.
Last updated 1998.08.22.
 (3-y)/3 - 4y + 1-
(3-y)/3 - 4y + 1-  (3-y)/3 = 3. By making two mistakes in this line, she brings out y = 3/2. Try it again, oh VIS INERTIAE! Away with INERTIAE: infuse a little more VIS: and you will bring out the correct (though uninteresting) result, 0 = 0! This will show you that it is hopeless to try to coax any one of these 3 unknowns to reveal its separate value. The other competitor, who is wrong throughout, is either J. M. C. or T. M. C.: but, whether he be a Juvenile Mis-Calculator or a True Mathematician Confused, he makes the answers 7d. and 1s. 5d. He assumes, with Too Much Confidence, that biscuits were
(3-y)/3 = 3. By making two mistakes in this line, she brings out y = 3/2. Try it again, oh VIS INERTIAE! Away with INERTIAE: infuse a little more VIS: and you will bring out the correct (though uninteresting) result, 0 = 0! This will show you that it is hopeless to try to coax any one of these 3 unknowns to reveal its separate value. The other competitor, who is wrong throughout, is either J. M. C. or T. M. C.: but, whether he be a Juvenile Mis-Calculator or a True Mathematician Confused, he makes the answers 7d. and 1s. 5d. He assumes, with Too Much Confidence, that biscuits were  d. each, and that Clara paid for 8, though she only ate 7!
d. each, and that Clara paid for 8, though she only ate 7! , and s =
, and s = 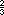 ,
, 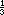 , giving the result,
, giving the result,  which is nearer to 9/10 than if he had used method (a).
which is nearer to 9/10 than if he had used method (a).