| 1000-Level | ....... | 2000-Level | ....... | 3000-Level | ....... | 4000-Level |
This course has been renumbered as MATH 4790H[409H] .
This course has been split into MATH 4120H[412H] and MATH 4130H[413H]

A chain of vortices twist in fluid flowing past a cylinder.
[Image courtesy of Chris Were]
This course provides an introduction to the mathematical modeling process and applies this process to simple mathematical modeling problems arising from a variety of application areas in science and engineering. Mathematical modeling techniques, such as differential equations, dimensional analysis, discrete systems and numerical methods along with computer aids will be utilized.
- Prerequisite: MATH-PHYS 2150H[205H] .
- Meetings: Two hours weekly.
- Class timetable:
- Instructor:
- For more information, please see the MATH 4120H homepage.
This course further develops the mathematical modelling techniques introduced in MATH 4120H[412H] . Emphasis will be placed on partial differential equation models such as diffusion processes, wave motions and fluid flows.
- Prerequisite: MATH 4120H[412H] and one of MATH PHYS-305H, or MATH PHYS-308H.
- Meetings: Two hours weekly.
- Class timetable:
- Instructor:
- For more information, please see the MATH 4130H homepage.
Description:
This course covers a variety of advanced Applied Mathematics techniques, which are fundamental tools for many areas of application in the physical sciences and engineering. The main topics include regular and singular perturbation methods for algebraic and differential equations and asymptotic methods for differential equations and integrals. Due to nonlinearity and geometric complexity, it is often impossible to obtain exact solutions for problems of significant interest. The study of asymptotic and perturbation methods provides a systematic approach for the construction of approximate solutions and analysis to these otherwise mathematically intractable problems.
This course will be a significant asset for any student going onto graduate studies in Applied Mathematics.
Schedule of topics:
- Introduction:
- Theory, definitions, terminology.
- Asymptotic sequence and series.
- Convergence.
- Dimensional analysis:
- Scaling
- Buckingham Pi theorem.
- Algebraic/Transcendental equations:
- Regular and singular perturbation methods.
- Asymptotic expansion of integrals:
- Laplace's method
- Watson Lemma.
- Methods of stationary phase.
- Methods of steepest descent.
- Asymptotic expansion of ordinary differential equations:
- Regular and singular perturbation problems.
- Applications.
- Asymptotic expansion of partial differential equations:
- Regular and singular perturbations.
- Boundary layer theory.
- Outer-inner solutions.
- Asymptotic matching.
- Prerequisite: MATH-PHYS 2150H[205H] and MATH-PHYS 3160H[303H] .
- Meetings: Three lectures and one tutorial weekly.
- For more information, please see the MATH 4160H homepage.
- Class timetable:
- Instructors:
Description:
The mathematical modelling of most problems arising from the physical sciences and engineering often leads to ordinary and partial differential equations for which exact solutions cannot be found. Therefore, numerical methods must be employed to obtain accurate approximations of these solutions. This course covers commonly used numerical techniques for solving differential equations including adaptive, multi-step and finite difference methods. Numerical stability, convergence and the issue of solution consistency would also be covered.
This course, or its equivalent, is typically required or highly recommended for students entering graduate schools in Applied Mathematics and is a very useful course for students from other Natural Science departments such as Physics and Chemistry.
Schedule of topics:
- Introduction:
- Review of ordinary and partial differential equations.
- Numerical differentiation and integrations.
- Numerical solutions of ordinary differential equations:
- Euler's, Taylor and Runge-Kutta methods.
- Multi-step methods.
- Stiff equations and stability.
- Adaptive methods.
- Numerical solutions of partial differential equations:
- Finite difference methods: Elliptic, Hyperbolic and Parabolic equations.
- Explicit and implicit iterative methods for matrix equations.
- Stability and error analysis.
- Nonlinear equations.
- Introduction to finite-element methods.
- Prerequisite: MATH-COIS 2180H[203H] and MATH-PHYS 2150H[205H] .
- Meetings: Three lectures and one tutorial weekly.
- For more information, please see the MATH 4180H homepage.
- Class timetable:
- Instructors:
|
An introduction to the syntax and semantics of propositional and first-order logics through the Soundness, Completeness and Compactness Theorems.
|
An introduction to computability via Turing machines and recursive functions, followed either by applications to the Incompleteness Theorem or by an introduction to complexity theory.
- Prerequisite: COIS 305H or MATH 3332H or 336H or MATH-COIS 4215H or permission of the instructor.
- Class timetable:
- Instructor:
Description: This course can cover any topic in geometry not covered by one of our other courses; the syllabus will be determined by the interests of the instructor and students. However, usually, MATH 4260H[426H] is offered as a course in Projective Geometry.
Projective geometry originated during the Renaissance, to deal with the mathematical problems of perspective drawing. Loosely speaking, projective geometry concerns the geometry of lines and planes as seen `from infinitely far away'.
Rough Syllabus:
- Incidence structures, affine and projective planes
- Constructing projective planes from affine planes and skew fields
- Combinatorial properties of projective planes
- Collineations, transitivity, Desargue's Theorem
- Introduction of coordinates, ternary rings
- Relations between geometric and algebraic properties
- Constructing projective planes using free completions
Text: A Problem Course on Projective Planes, Version 0.3, by Stefan Bilaniuk.
For more information, see the MATH 4260H[426H] Projective Geometry homepage
Prerequisite: MATH 2260H or MATH 3260H
- Meetings: To be arranged
- Timetable:
- Instructor:
- For more information, please see the MATH 4260H homepage.
Extension fields and Galois groups.
- Prerequisite: MATH 3320H[332H] .
- Recommended: MATH 3360H[336H] .
- Meetings: To be arranged.
- Class Timetable:
- Instructor: .
- Prerequisite: MATH 3320H[332H] or MATH 3360H[336H] .
- Meetings: To be arranged
- Class Timetable:
- Instructor:
Description: Given a topological space X (e.g. a surface in R3), we can define a group G(X) whose elements represent certain `geometric structures' within X (e.g. closed paths, embedded simplices, embedded spheres, etc.). The multiplication operator of G(X) also has a natural geometric interpretation (e.g. concatenation of two paths), and thus, the algebraic structure of G(X) reflects the `global' topological properties of X. In particular, a continuous function between two topological spaces X and Y induces a group homomorphism between G(X) and G(Y) respective groups. Because of this, G(X) is called an algebraic invariant of X. For example, we can detect that X and Y are not homeomorphic if we can show that G(X) and G(Y) are not isomorphic (which is usually easier).
Algebraic topology is the construction, analysis, and computation of such algebraic invariants of topological spaces. It lies at the interface between algebra and topology. Algebraic topology topology also provides a unified framework which encompasses and explains such diverse phenomena as Stokes Theorem in Differential Geometry (MATH 3720H[302H] ), the Cauchy Residue Formula in Complex Analysis (MATH 3770H[307H] ), or Euler's formula for planar graphs in Graph Theory (MATH 4610H[461H] ) .
Algebraic topology is an important area of contemporary mathematical research, and is highly relevant to any student entering graduate studies in pure mathematics.
The computational machinery underlying most of algebraic topology is a kind of abstract group theory called homological algebra. In this course, we will develop the basic concepts and methods of algebraic topology, and introduce the relevant homological algebra to support them.
Syllabus:
- Homotopy Groups: Homotopy of paths and functions. The Fundamental Group.
- Free and amalgamated products of groups. Connected sums of spaces. The Seifert-van Kampen theorem.
- Covering spaces and covering transformations.
- Higher homotopy groups. Categories and functors.
- Homological Algebra: Chain complexes and long exact sequences. Homology of a chain complex.
- Simplicial complexes: triangulation of surfaces and barycentric subdivision. Euler characteristic; the classification of closed surfaces.
- Simplicial Homology groups: definition & examples. Relative homology groups and excision;
- Simplicial homology groups: Mayer-Vietoris sequences. Betti numbers and torsion coefficients. Euler-Poincaré characteristic.
- Simplicial cohomology: Definition and examples.
- Poincaré duality theorem.
- Applications to smooth dynamics: Brouwer fixed point theorem,
- Review. Time permitting: Cap products and cohomology rings. Other (co)homology theories (e.g. (co)bordism, de Rham cohomology, etc.) Eilenberg-Steenrod axioms.
- Prerequisite: MATH 2110H[201H] and MATH 3320H[332H] .
- Suggested corequisites: MATH 2120H[202H] , MATH 3720H[302H] , or MATH 3770H[307H] .
Probable Text: A Combinatorial Introduction to Topology, by Michael Henle (Dover, 1994).
Auxiliary Text: Algebraic Topology, by Allen Hatcher (Cambridge UP, 2002).
- Meetings: Three lectures and one tutorial weekly.
- For more information, please see the MATH 4330H homepage.
- Class Timetable:
- Instructors:
Description: Linear algebra is the oldest part of modern abstract algebra, and a source of many motivating problems and concrete examples in the theory of groups and rings. Conversely, however, advanced linear algebra yields powerful tools to learn more about groups and rings (such as modules and linear groups). Furthermore, advanced linear algebra is of central importance in differential geometry (via tensor algebra and Lie theory) and differential equations (via canonical forms and Lie theory) and also functional analysis. Thus, it is crucial background knowledge for any student entering graduate studies in pure or applied mathematics, or in mathematical physics.
We begin with multilinear algebra, which underlies all of modern differential geometry and much of modern functional analysis (and hence, indirectly, general relativity and quantum mechanics). We then study the rich geometric structure of linear groups (i.e. groups of invertible matrices). Linear groups are the simplest examples of Lie groups, which lie at the interface between group theory and differential geometry. Lie theory is not only intrinsically beautiful, but also a powerful tool to study smooth dynamical systems and the symmetries of Riemannian manifolds.
A module is like an abstract vector space, except that the `scalars' only form a ring instead of a field. In other words, the scalars do not necessarily have multiplicative inverses. For example, any abelian group is a module (with the scalars being the ring of integers). Let R[x] be the ring of polynomials with real coefficients. If V is a real vector space and T:V---> V is a linear transformation, then T makes V into a module over R[x], and the structure of this module allows us to find a two `canonical' matrices to represent T, the rational canonical form and Jordan canonical form. These canonical forms are useful for two reasons:
(For both reasons, canonical forms are critically important in the qualitative theory of ordinary differential equations).
- They reveal important structural information about the transformation T (e.g. its eigenvalues and eigenspaces).
- They reveal when two linear transformations are conjugate (i.e. identical after a suitable change of basis).
We next turn group representation theory. A representation of an abstract group G is a homomorphism from G to some linear group. Representations provide a powerful tool to study the structure of abstract groups, and are important in harmonic analysis and quantum physics. Finally, time permitting, we introduce projective and injective modules, which play a central role not only in representation theory, but also in homological algebra, and hence, in algebraic geometry and algebraic topology.
- Prerequisite: MATH 3360H[336H] .
- Recommended: MATH 3320H[332H] .
Probable Text: Chapters 7, 8, 9, and 12 of Algebra by Michael Artin (1991, Prentice-Hall)
or Chapters 10, 11, 12 and 15 of Abstract Algebra by David S. Dummit and Richard M. Foote (3rd edition, 2004, Prentice-Hall)- Meetings: Three lectures and one tutorial weekly.
- For more information, please see the MATH 4350H homepage.
- Class Timetable:
- Instructors:
This course has been discontinued.
Description: An algebraic variety is a shape in space which arises as the solution-set to an algebraic equation. For example, the unit circle in R2 is the set of all solutions to the equation ; thus, the unit circle is an algebraic variety. Of course, algebraic varieties can become much more complicated than this. Algebraic geometry studies the geometry of algebraic varieties using algebraic methods (primarily the theory of commutative rings).
Algebraic varieties are closely related to (but not the same as) differentiable manifolds. For example, the circle is both a variety and a manifold. Indeed, an algebraic variety locally `looks like' a manifold almost everywhere, except possibly at a small set of `singular points' such as `cusps' (sharp corners) or `self-intersections' (places where two branches of the variety passes through each other). Thus, algebraic geometry and differential geometry are closely related, yet complimentary in their methods. Indeed, most of the interesting research in modern geometry involves a fusion of algebraic and differentiable methods.
The beauty and elegance of algebraic geometry arises from the surprising and powerful ways in which geometric information is encoded algebraically. For example, almost everything you want to know about the geometry of a variety is encoded in the ideal structure of an associated polynomial ring. Thus, algebraic geometry brings to bear the full power of modern abstract algebra (primarily the theory of commutative rings; see MATH 3360H[336H] ) to obtain geometric insights. It is thereby fulfils Sophie Germain's aphorism: ``Algebra is no more than geometry in writing; geometry is no more than algebra in pictures.''
Possible Syllabus:
- The projective space P2 and affine space A2. Planar conics. Bezout's Theorem.
- Linear systems of conics. Cubic curves; cubics in general position.
- Group law on a cubic. Genus of curves. Noetherian rings, Hilbert Basis theorem. Affine varieties. Zariski Topology.
- Hilbert's Nullstellensatz.
- Coordinate rings; (iso)morphisms; affine varieties. Rational functions.
- The addition law on elliptic curves. Prime spectra and maximal spectra.
- Nilpotents and nilradicals; local rings
- Modules. Homomorphisms and isomorphisms. Nakayama's lemma. Exact sequences.
- Noetherian rings and Noetherian modules.
- Projective varieties. Quadric and Veronese surfaces. Birational equivalence
- Tangent spaces and nonsingular points. Resolution of singularities.
- The 27 lines on a cubic surface
Prerequisite or Corequisite: MATH 2110H[201H] and MATH 3360H[336H] .
Probable Text: Undergraduate Algebraic Geometry, by Miles Reid
Auxiliary Text: Undergraduate Commutative Algebra, by Miles Reid
Meetings: Three lectures and one seminar weekly.
- For more information, please see the MATH 4370H homepage.
- Class Timetable:
- Instructors:
This course has been renumbered as MATH 4700H[410H] .
Description: This course covers the basic mathematical theory and computational techniques for how financial institutions can quantify and manage risks in portfolios of assets.
Syllabus:
- Introduction
- Portfolios
- Defining Risk
- Complete and Incomplete Markets
- Market Efficiency
- Mean-Variance Analysis
- Asset Return
- Portfolio Mean and Variance
- Efficient Frontier
- Markowitz Minimum Variance Portfolio
- One-Fund/Two-Fund Theorems
- Inclusion of Risk Free Assets
- Non-Linear Optimization
- Capital Asset Pricing Model (CAPM)
- Capital Market Line
- Beta Factor
- Security Market Line
- CAPM as a Pricing Formula
- Models and Data
- Data and Parameter Estimation
- Forecasting Volatilities and Correlations
- Risk Measurement
- Value at Risk (VaR)
- Credit Risk
- Computational Techniques
- Prerequisite: MATH 1550H[155H] and MATH 2150H[205H] . Excludes MATH 451H.
- Meetings: Three lectures and one tutorial weekly.
- For more information, please see the MATH 4510H homepage.
- Class Timetable:
- Instructors:
This course has been reincarnated as MATH 4560H[456H] Topics in Statistics.
This course has been reincarnated as MATH 4560H[456H] Topics in Statistics.
(formerly MATH 4510H[451H] /452)
- Prerequisites: MATH 2560H.
- Strongly Recommended: MATH 3560H.
- Meetings: To be arranged
- Class Timetable:
- Instructor:
- For more information, please see the 4560 web page.
- Prerequisites: MATH 2560H (256H), with at least 60% or permission of instructor..
- Recommended: MATH 3560H (356H). Excludes MATH 456H.
- Meetings: To be arranged
- Class Timetable:
- Instructor:
- For more information, please see the 4561 web page.
The goal of this course is to introduce students to the principles and methods of designed experiments. Designs commonly used in research will be studied, with focus both on analysis and construction of designs. Students will apply the concepts studied in applications.
- Prerequisites: MATH 2560H (256H), with at least 60% or permission of instructor..
- Recommended: MATH 3560H (356H). Excludes MATH 456H.
- Meetings: To be arranged
- Class Timetable:
- Instructor:
- For more information, please see the 4562 web page.
and data analysis
Students enrolled in this course will follow the course syllabus for BIOL-ERSC 403H (please consult course description for the latter) . Students registered in MATH 4563H will complete assignments for BIOL-ERSC 403H, with theoretical assignments replacing some of the labs required there.
- Prerequisites: MATH 2560H (256H), with at least 60% or permission of instructor..
- Recommended: MATH 3560H (356H). Excludes MATH 456H.
- Meetings: To be arranged
- Class Timetable:
- Instructor:
- For more information, please see the 4563 web page.
This course is dedicated to the study of more advanced models in the theory of stochastic processes. These include renewal processes, martingales and Brownian motion. The course concludes with a basic introduction to stochastic calculus.
- Prerequisite: MATH 3570H[357H] .
- Meetings: Three lectures per week
- Class Timetable:
- Instructor:
- For more information, please see the 4570 web page.
This course has been split into MATH 4610H[461H] and MATH 4620H[462H] .
An introduction to graph theory with emphasis on both theory and applications and algorithms related to computer science, operation research and management science.
- Prerequisite: MATH-COIS 2600H[260H] or permission of the instructor.
- Meetings: Three hours weekly.
- Class Timetable:
- Instructor:
- For more information, please see the MATH 4610H[461H] home page.
An introduction to combinatorics. The topics include counting techniques, generating functions and block design.
- Prerequisite: MATH-COIS 2600H[260H] or permission ofthe instructor.
- Recommended: Mathematics 330.
- Meetings: Three hours weekly.
- Class Timetable:
- Instructor:
- For more information, please see the MATH 4620H[462H] home page.
This course has been split into
MATH 4710H[471H]
and
MATH 4720H[472H] .
(Formerly MATH 4370H[437H] )
- Prerequisite: MATH 3700H[310H] .
- Meetings: To be arranged
- Class Timetable:
- Instructor:
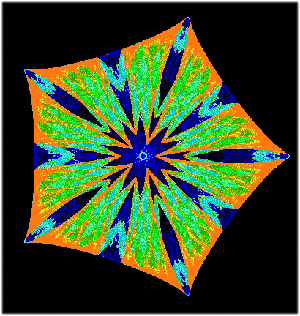
A symmetric attractor of a D5-equivariant dynamical system |
|
We will cover the following topics:
- Basic topological dynamics: Orbits, fixed and periodic points, attraction and repulsion, basins of attraction.
- One dimensional systems: Piecewise linear maps, logistic parametrised families, Baker maps.
- Bifurcations: Definition, examples. The Feigenbaum constant and Feigenbaum universality. The Schwarzian derivative (which enables us to theoretically explain some aspects of bifurcation diagrams).
- Chaos: Sensitivity to initial conditions; Lyapunov exponents.
- Basic symbolic dynamics: Partitions and itineraries. Conjugacy. Applications to chaos.
- Fractals: Deterministic fractals generated as fixed points of iterated function systems. Various definitions of fractal dimension.
- Prerequisite: MATH 3700H[310H] or permission of the instructor.
- Meetings: Three hours of lecture and one seminar weekly.
- Class Timetable:
- Instructor:
- Probable Text: Chaos by Kathleen T. Alligood, Tim D. Sauer and James A. Yorke.
|
This course continues MATH 4710H[471H] . We will cover the following topics:
|
 The Julia set for . As moves, the Julia set changes. |
 The Riemann surface of the complex cube root function. |
Some selection of the following topics:
|
(Formerly Math 406H)

The Sierpinski triangle has Hausdorff dimension |
Some selection of the following topics:
|
- Prerequisites: MATH 3790H[309H] and MATH 3700H[310H] .
- Meetings: Three hours weekly.
- Class Timetable:
- Instructor:
A survey of current research areas in mathematics, with two-week introductions to a variety of topics.
- Prerequisites: MATH 2110H[201H] , MATH 2120H[202H] , MATH 2350H[235H] , one full mathematics credit (e.g. two half-courses) at the 300 level.
- Class Timetable:
- Instructor: Several faculty members will participate
A survey of current research areas in mathematics, with two-week introductions to a variety of topics.
- Prerequisites: MATH 2110H[201H] , MATH 2120H[202H] , MATH 2350H[235H] , one full mathematics credit (e.g. two half-courses) at the 300 level.
- Class Timetable:
- Instructor: Several faculty members will participate
Students are placed in research projects with community organizations in the Peterborough area. Each placement is supervised jointly by a faculty member and a representative of a community organization. For details see the section on Community-based education program in the Academic Calendar.
- Prerequisites: MATH 2560H (256H), and either MATH 3560H (356H) or MATH 4561H or MATH 4562H.
- Note: Open only to students who have a cumulative average of at least 75%.
- Meetings: To be arranged
- Class Timetable:
- Instructor:
- For more information, please see the 4850 web page.
Game theory is the mathematical analysis of strategic interactions between rational agents. These interactions could be `recreational' games (e.g. chess, poker), but we are more interested in political, economic, military, or ecological interactions. The `agents' could be consumers, voters, firms, governments, armies, or co-evolving species. Their strategic interactions might be cooperative (e.g. trade, symbiosis) or competitive (e.g. oligopoly, warfare), but are usually some mixture of the two.
Game theory starts with the assumption that all agents are perfectly rational, with precisely defined objectives. Each agent can thus always identify her `best response' to any strategy chosen by the other agents. Each agent also knows that the other agents are rational with well-defined objectives; thus, she can predict that they will deploy their best responses to her best response. She will therefore adapt her best response to their best responses to her best response, and so on. This process of mutual adaptation terminates in a Nash equilibrium, where every agent's strategy is a best response to the strategies of all the other agents. The Nash equilibrium is the fundamental analytic tool of game theory.
There are many refinements to the Nash equilibrium concept, depending upon what additional assumptions we make. Does the game terminate instantaneously after each player `moves' exactly once? Or does the game unfold over time? Do the agents have perfect knowledge about each other's strategies, or is some information secret? Do they have perfect knowledge of one another's objectives, or can they only guess? Are the agents infallible, or do they sometimes make mistakes? And if they know that they might make mistakes, how does this affect their strategy? Can the players form `coalitions'? How can they trust each other? What if they don't?
Game theory provides a powerful analytical methodology, which has become ubiquitous in economics, political science, military theory, philosophy and evolutionary biology.
- Class Timetable:
- Instructor:
- Meetings: Three hours of lecture and one hour seminar per week.
- Prerequisites: Math 2110H[201H], 2200H[220H] and Math 2350H[235H]; or Econ 300H and Econ 325H.
- Probable Text: A course in game theory, by Martin J. Osborne and Ariel Rubinstein (1994, MIT press).
Game Theory: Analysis of Conflict, by Roger B. Myerson (1991, Harvard UP). - Note: This is an experimental trial of a new course. This course will only be offered if there is sufficient student demand.
- Prerequisite: Permission of the instructor.
- Meetings: To be arranged.
- Instructor:
This is a seminar-based course in problem solving in which participants will work on a diverse assortment of mathematical problems. The focus will be on presenting clear, mathematically correct solutions to problems. Most of the problems will be of a type not normally encountered in other courses and, although the problems themselves will not require sophisticated techniques, their solutions will not usually be straightforward
What's the best way for society to make collective decisions? What voting system is the fairest? Most rational? Most democratic? These questions were first studied by the mathematicians Borda and Condorcet in 18th century France. In 1950, Kenneth Arrow proved a shocking theorem: it is impossible to design an `ordinal' voting system (where voters rank their `first', `second', `third' choices, etc.) which is both `fair' and `rational'. Arrow's theorem explains much of what goes wrong in real-world democracies.
Arrow's theorem does not say that `Democracy is impossible'; it simply says that we must use richer information about voters' preferences if we want sensible outcomes. In the late 18th century, British philosopher Jeremy Bentham argued for utilitarianism: society should choose the policies which lead to the greatest total happiness (`utility') when summed over all citizens. A precise mathematical definition of `utility' was provided by John von Neumann and Oskar Morgenstern in 1949, and Bentham's utilitarian intuitions were formalized by the economist John Harsanyi in the 1950s. However, in 1970, the philosopher John Rawls argued instead for egalitarianism: society should choose the policy which maximizes the utility of its least fortunate members. Utilitarianism and egalitarianism are both examples of social choice functions ---rules for guiding social policy. But which rule is best?
Voting is not the only form of collective decision-making; many decisions are made through bargaining between two or more parties. Suppose you are asked to arbitrate between the parties; what is the fairest settlement you can propose? Utilitarianism and egalitarianism both suggest answers to this question, but in 1950, John Nash discovered a `bargaining solution' which is optimal in a mathematically precise way. The Nash bargaining solution yields another social choice function, which compromises between utilitarianism and egalitarianism.
Since the work of these pioneers, social choice theory has grown into a major modern research area, at the interface between mathematics, economics, and political philosophy. It uses mathematics to confront problems which lie at the heart of contemporary political and economic disputes.
- Instructor:
- Timetable:
- Meetings: Three hours of lecture and one hour seminar per week.
- Probable Texts: Two of:
- Primary: Axioms of Cooperative Decision-Making, by Hervé Moulin. (1988, Cambridge UP)
- Secondary: A Primer in Social Choice Theory, by Wulf Gaertner (2006, Oxford UP).
- ...and possibly some preprinted lecture notes by the instructor.
- Probable Grading Scheme: Best 8 out of 9 quizzes, plus year-end research paper and presentation.
- Prerequisites:
| 1000-Level | ....... | 2000-Level | ....... | 3000-Level | ....... | 4000-Level |

