|
|
|
Math.-Physics 305H |
Partial Differential Equations
| Fall 2004 |
-
Prerequisite: Mathematics 205H.
- Corequisite: Mathematics 200.
- Meetings: Three hours weekly.
- Class timetable
- Instructor:
-
For more information, please see the MATH 305 home page.
Synopsis: We'll focus on the following topics:
- The Heat equation, Wave
equation, Laplace equation, and Poisson equation in one, two, and
three dimensions, in Cartesian, Polar, and Spherical
coordinates.
- Solution methods using eigenfunction expansions (Fourier
series, Fourier transforms, Bessel functions)
- Solution methods using convolutional
transforms (Gauss-Weierstrass kernel, d'Alembert method).
|

The Wave Equation: A vibrational mode of a circular membrane. |
|
Overview: Partial differential equations (PDEs) model physical systems which
evolve continuously in time, and whose physical state is described by
some continuous function in space. For example, suppose we pour some
ink into a flat tray of water. Let describe the
concentration of ink in the tray at spatial coordinates and
time . Then the ink obeys the Heat Equation:
| d p | | d2 p | | d2 p |
| ------ | = | ------ | + | ------ |
| d t | | d x2 | | d y2 | |
This equation says the ink will diffuse from regions of
high concentration to regions of low concentration until it is uniformly
distributed throughout the pan.
| |
PDEs are ubiquitous in applied mathematics. For example:
- In physics: The Schrodinger equation describes the
evolution of a quantum wavefunction. The Einstein equation
describes the curvature of space-time.
- In chemistry: Reaction-diffusion equations describe spatially
distributed chemical systems.
- In biology: PDEs describe ontogenic processes and ecosystems.
Given a PDE we can ask four questions:
- Do solutions exist?
- Is the solution unique?
- What is an explicit formula describing the solution?
- What is the long-term qualitative behaviour of the system?
|
|
Math. 306H |
Analysis II: Complex Analysis
| Discontinued |
This course has been renamed Math 307H,
and moved to the Fall semester.
|
|
Math. 307H |
Analysis II: Complex Analysis
(formerly Math 306H)
| Fall 2004 |
`Complex' analysis should really be called `simple' analysis
because of its incredible beauty and elegance. Those who study complex
analysis find themselves suspecting that we were `supposed' to live in
a complex universe, but we got stuck in a `real' universe by
some terrible cosmic accident.
In this course, we will emphasise the geometric interpretation of
complex-analytic concepts. We will cover the following topics:
- Complex arithmetic and the complex plane; geometric interpretation.
- Complex functions as transformations of the complex plane:
polynomials, the exponential map, trigonometric functions.
- Power series. Radius of convergence. How a complex singularity
can affect a real power series.
- Complex multifunctions: fractional powers and the complex logarithm.
Branch points and Riemann surfaces.
- Complex differentiation: The derivative as `Amplitwist'.
Conformal maps. The Cauchy-Riemann Equations.
- Winding numbers and Hopf's degree theorem. Path homotopy.
- Complex contour integrals; Cauchy's theorem.
- The Cauchy Residue formula. Calculus of Residues; Laurent series.
- The Argument Principle. Darboux' Theorem. Rouché's Theorem.
The Fundamental Theorem of Algebra
- The Maximum Modulus Principle. Liouville's theorem.
- (Time permitting) Introduction to Möbius transformations
and the Riemann sphere.
|
|

Colour-coding the complex plane in polar coordinates

The complex exponential map, seen through this colour-coding. |
|
|
Math.-Physics 308H |
Methods of applied mathematics |
Winter 2005 |
|
Differential equations in applied mathematics, including Bessel,
Legendre, hypergeometric, Laguerre, Hermite, Chebyshev, etc. Series and
numerical solutions. Properties of the special functions arising from these
equations.
-
Prerequisite: Mathematics-Physics 205H.
- Meetings: Three lectures and one tutorial weekly.
- Instructor:
-
For more information, please see the
MATH 308 home page.
|
|
Math. 309H |
Analysis I: Introduction to Analysis
(formerly Math 206H)
| Fall 2004 |
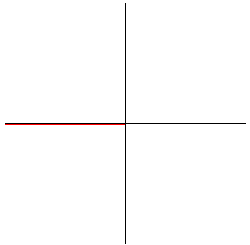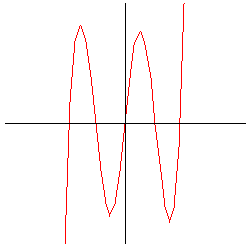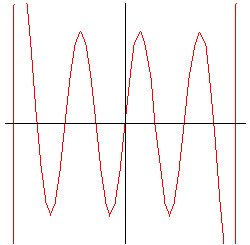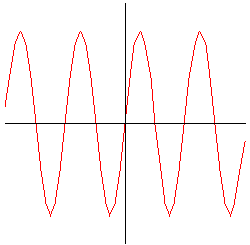
A sequence of successively higher order Taylor polynomials converge to the sine function. |
The real number system. Limits. Continuity. Differentiability.
Mean-value theorem. Convergence of sequences and series. Uniform convergence.
-
Prerequisite: Mathematics 110.
- Corequisite: Mathematics 201H.
- Meetings: Three hours weekly.
- Class timetable
- Instructor:
|
|
|
Math. 310H |
Topology I: Metric spaces
| Winter 2005 |
|
Limits and continuity. Completeness, compactness, the Heine-Borel
theorem. Connectedness.
|
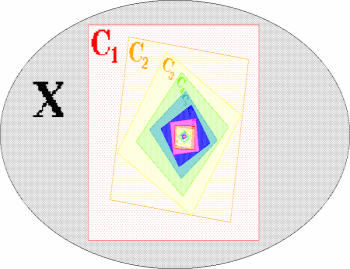
The Chinese Box Theorem says: if is a descending sequence of
compact sets, then their common intersection is nonempty.
This implies that every contraction mapping on a compact space has a
fixed point. |
|
|
Math.-Physics 311H |
Advanced classical mechanics
| Winter 2005 |
|
Applied mathematics as found in the classical mechanics of particles,
rigid bodies and continuous media. Motion of rigid bodies, Lagrangian mechanics,
Hamiltonian mechanics, dynamics of oscillating systems.
|
|
Math.-Physics 312H |
Classical mechanics
| Fall 2004 |
|
Applied mathematics as found in the classical mechanics of particles.
One-dimensional motion, vector differential operators, three-dimensional
motion, moving and rotating coordinate systems, central forces, systems
of particles.
-
Prerequisites: Mathematics 110 and Physics 100 or permission of
the instructor.
-
Pre or co-orequisite: Mathematics 200.
- Meetings: Three lectures and tutorial weekly.
- Class timetable
-
Taught by the Department
of Physics.
|
|
Math. 322 |
Number Theory
|
Not offered in 2004-2005
|
-
Prerequisites: Mathematics 110, and 130 or 235H.
- Meetings: Three hours weekly.
- Class timetable
- Instructor: Not offered
Overview: Number theory is one of the oldest and richest areas of mathematics,
and ubiquitous in contemporary mathematical research. We will likely examine
the following topics:
Prime Numbers:
The Fundamental Theorem of Arithmetic says every number has
a unique factorization into primes. We'll prove this theorem, and
study its consequences.
- How many primes are there? Euclid proved there are an infinite
number.
- How `densely' are the primes distributed in the natural numbers?
Let be the number of primes less than . For example,
, because the primes less than 24 are
The Prime Number Theorem states:
This says that
In other words, approximately 7.2% of the numbers less than 1 000 000 are
prime.
- Are there patterns in prime numbers? Are there
formulas for generating them? Is there
an efficient way to test whether a given number is prime?
- RSA encryption uses prime factorization to create
a public-key cryptosystem. An efficient factorization algorithm would
break the encryption. We'll discuss this.
Diophantine Equations: A Pythagorean triple is a triple
of integers so that .For example: .
Such numbers are called Pythagorean because they form the sides
of a right-angle triangle. Such triples are quite
hard to construct.
| |
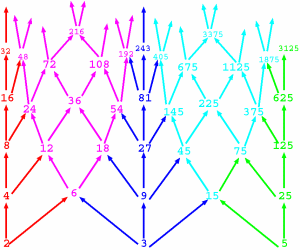
The Lattice of Divisibility of integers.
The equation (with the stipulation that be integers)
is an example of a Diophantine Equation. Such equations are
very hard to solve. Another famous Diophantine
equation is the Fermat Equation:
.
Fermat's famous Last Theorem says this equation
has no nontrivial solutions for .
Modular arithmetic is the arithmetic of 12 hour clocks,
7 day weeks, etc., and is fundamental to the theory of groups and
rings. We will develop the basic theory of congruence relations. We
will then look into congruence equations, focusing on such
topics as:
- Fermat's Little Theorem and Wilson's Theorem.
- The Chinese Remainder Theorem, which solves systems of
linear congruence equations.
- Quadratic congruences and the Quadratic Reciprocity theorem.
- Lucas' theorem, which describes the binomial
ceofficients, mod , and has applications to cellular automata.
|
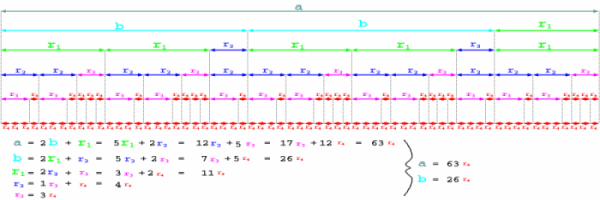
The Euclidean algorithm is a method to compute the
greatest common divisor of two numbers.
|
|
|
Math. 326H |
Geometry II: Projective & non-Euclidean geometries
| Not offered in 2004-2005 |
|
Elements of projective and non-Euclidean geometries, including
an introduction to axiomatic systems.
- Prerequisite: Mathematics 135H or permission of the instructor.
- Meetings: Two lectures and one tutorial weekly.
- Offered in alternate years but not in 2004-2005.
|
|
|
Math. 330 |
Algebra III: Groups, rings & fields
| Fall-Winter 2004-2005 |
|
Overview:
We will study three kinds of algebraic structures: groups, rings, and fields.
Group Theory:
Groups encode the symmetries other objects. For example:
- Dihedral groups describe the symmetries of figures in the plane.
- Polyhedral groups describe the symmetries of polyhedra
in three dimensions.
- Tiling groups describe the symmetries of infinite tilings of the plane.
- Linear Groups describe symmetries of objects in Euclidean
space of many dimensions.
- Lie Groups describe the symmetries of curves, surfaces, and
other manifolds.
Groups can also be thought of as `abstract spaces', or used to encode
geometric/topological information. For example
- Vector spaces are groups with an explicitly spatial structure.
- Homotopy groups describe how curves can continously deform
in a surface or other space. They encode information about the
topology of the space.
- Holonomy groups describe the distortions introduced by traveling
through curved space.
Ring Theory:
Rings are algebraic structures which encode abstract arithmetic.
- Number rings extend the arithmetic of integers.
Many problems in number theory (eg. Fermat's Last Theorem) can be
better understood by contextualizing them within ring theory.
- Coordinate rings describe the geometry
of a curve, surface, or other space.
Many geometric questions about the space can be translated into
algebraic questions about the ring, and answered using algebraic
methods.
- Operator Algebras: are rings of matrices acting on a
vector space. They arises in areas from dynamical systems to quantum
theory.
Field Theory:
A field is a special kind of ring with a particularly
rich algebraic structure. The rational numbers, the real numbers,
and the complex numbers are examples of fields. Field theory reveals
important limitations to mathematical methods. For example:
- You can't trisect an angle or construct a 7-gon using a compass
and straightedge. It's not that we haven't figured it out yet;
you simply can't.
- You can solve any quadratic equation with
the Quadratic Formula. However,
there is no analogous quintic formula for solving a quintic equation
. It's not that we haven't found it yet;
there simply isn't one.
|
|
| 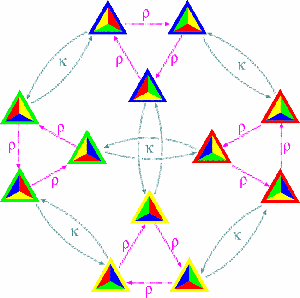
The group of symmetries of a tetrahedron
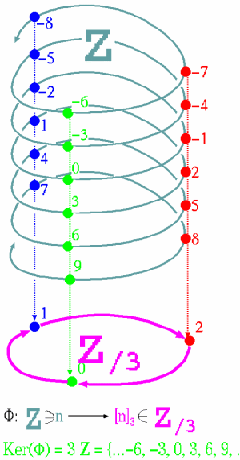
A group epimorphism from
into Z/3
|
|
|
Math.-Comp. Sci. 341 |
Linear and discrete optimization
| Fall-Winter 2004-2005 |
|
Introduction to the concepts, techniques and applications of linear
programming and discrete optimization. Topics include the simplex method,
dynamic programming, duality, game theory, transportation problems, assignment
problems, matchings in graphs, network flow theory, and combinatorial optimization
with emphasis on integer programming.
-
Prerequisites: Mathematics 130 or 135H, and Mathematics-Computer
Science 260.
- Meetings: Two lectures and one tutorial weekly.
- Class timetable
- Instructor:
-
For more information, please see the MATH 341 home
page.
|
Math. 355 |
An introduction to statistical analysis
| Discontinued |
This course has been replaced with
Math 256H in the fall
semester, and
with either Math 356H
or Math 357H during the winter semester.
|
|
Math.-Science 356H | Linear Statistical Models
|
Not offered in 2004-2005
|
|
Linear regression and correlation, multiple regression, analysis of variance
and experimental designs. Assumes a background in probability and uses
introductory linear algebra.
- Prerequisite: MATH 256H.
- Strongly recommended: MATH 135H.
- Class timetable
- Instructor: Not offered
- Three hours of lectures weekly.
|
|
Math.-Science 357H | Introduction to
Stochastic Processes
|
Winter 2005 |
|
This course covers a variety of important models used in modeling of random
events that evolve in time. These
include Markov chains (both discrete and continuous), Poisson processes and
queues. The rich diversity of
applications of the subject is illustrated through varied examples.
- Prerequisite: MATH 155H.
- Class timetable
- Instructor:
- Three hours of lectures weekly.
|
|
Math.-Science 380 |
History of mathematics
|
Not offered in 2004-2005
|
|
A study of the major currents of mathematical thought from ancient
to modern times.
-
Prerequisites: Mathematics 110 and 235H, or Mathematics 110 and permission of the instructor. Second-year students wishing to take the course must have permission of the instructor.
- Meetings: Three hours weekly.
- Class timetable
- Instructor:
-
For more information, please see the MATH 380 home page.
|
|
Math. 390 |
Reading-seminar course (Full) |
Fall and Winter (reading course) |
Details may be obtained by consulting the Department of Mathematics.
|
|
Math. 391H |
Reading-seminar course (Half) |
Fall or Winter (reading course) |
Details may be obtained by consulting the Department of Mathematics.
|
|
Math. 392H |
Reading-seminar course (Half) |
Fall or Winter (reading course) |
Details may be obtained by consulting the Department of Mathematics.
|
|
Math. 393H |
Reading-seminar course (Half) |
Fall or Winter (reading course) |
Details may be obtained by consulting the Department of Mathematics.
|
|
Math. 394H |
Reading-seminar course (Half) |
Fall or Winter (reading course) |
Details may be obtained by consulting the Department of Mathematics.
|
|










