3000-Level Mathematics Courses
at Trent University (2008-2009)

Notes:








1000-Level ....... 2000-Level ....... 3000-Level ....... 4000-Level
Math. 306H Analysis II: Complex Analysis Discontinued

This course has been renamed MATH 3770H[307H] , and moved to the Fall semester.

Math-Physics 308H Methods of applied mathematics Discontinued

This course has been renamed MATH-PHYS 3160H[303H]

Math.Phys 311H Advanced Classical Mechanics Discontinued

This course has been renamed MATH-PHYS 3140H[314H]

Math.Phys 312H Classical Mechanics Discontinued

This course has been renamed MATH-PHYS 3130H[313H]

MATH-PHYS 3150H[305H] Partial Differential Equations Fall 2008

Synopsis: We'll focus on the following topics:

  • The Heat equation, Wave equation, Laplace equation, and Poisson equation in one, two, and three dimensions, in Cartesian, Polar, and Spherical coordinates.
  • Solution methods using eigenfunction expansions (Fourier series, Fourier transforms, Bessel functions)
  • Solution methods using convolutional transforms (Gauss-Weierstrass kernel, d'Alembert method).

The Wave Equation: A vibrational mode of a circular membrane.

Overview: Partial differential equations (PDEs) model physical systems which evolve continuously in time, and whose physical state is described by some continuous function in space. For example, suppose we pour some ink into a flat tray of water. Let p(x,y;t) describe the concentration of ink in the tray at spatial coordinates (x,y) and time t. Then the ink obeys the Heat Equation:
d p d2 p d2 p
------ = ------ + ------
d t d x2 d y2
This equation says the ink will diffuse from regions of high concentration to regions of low concentration until it is uniformly distributed throughout the pan.

PDEs are ubiquitous in applied mathematics. For example:

  • In physics: The Schrodinger equation describes the evolution of a quantum wavefunction. The Einstein equation describes the curvature of space-time.
  • In chemistry: Reaction-diffusion equations describe spatially distributed chemical systems.
  • In biology: PDEs describe ontogenic processes and ecosystems.

Given a PDE we can ask four questions:

  1. Do solutions exist?
  2. Is the solution unique?
  3. What is an explicit formula describing the solution?
  4. What is the long-term qualitative behaviour of the system?

MATH-PHYS 3160H[303H] Methods of applied mathematics
(formerly Math 308H)		 Winter 2009

 Differential equations in applied mathematics, including Bessel, Legendre, hypergeometric, Laguerre, Hermite, Chebyshev, etc. Series and numerical solutions. Properties of the special functions arising from these equations.

MATH-PHYS 3130H[313H] Classical mechanics Fall 2008

 Applied mathematics as found in the classical mechanics of particles. One-dimensional motion, vector differential operators, three-dimensional motion, moving and rotating coordinate systems, central forces, systems of particles.

  • Prerequisites: MATH 1100[110] and Physics 100 or permission of the instructor.
  • Pre or co-orequisite: MATH 2110H[201H] .
  • Meetings: Three lectures and tutorial weekly.
  • Class timetable
  • Taught by the Department of Physics.

MATH-PHYS 3140H[314H] Advanced classical mechanics Winter 2009

 Applied mathematics as found in the classical mechanics of particles, rigid bodies and continuous media. Motion of rigid bodies, Lagrangian mechanics, Hamiltonian mechanics, dynamics of oscillating systems.

  • Prerequisites: MATH 2110H[201H] , and also MATH-PHYS 2150H[205H] and Mathematics-Physics 312H or 313H.
  • Meetings: Three class meetings weekly.
  • Class timetable
  • Taught by the Department of Physics.
MATH 3200H[320H] Number Theory Not offered 2008

Overview: Number theory is one of the oldest and richest areas of mathematics, and ubiquitous in contemporary mathematical research. We will likely examine the following topics: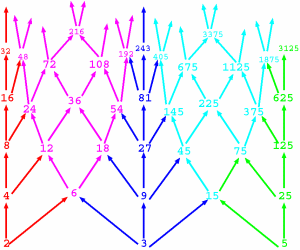

The Lattice of Divisibility of integers.

Prime Numbers: The Fundamental Theorem of Arithmetic says every number has a unique factorization into primes. We'll prove this theorem, and study its consequences.

  • How many primes are there? Euclid proved there are an infinite number.
  • How `densely' are the primes distributed in the natural numbers? Let P(n) be the number of primes less than n. For example, P(25)=9, because the primes less than 24 are {2,3,5,7,11,13,17,19,23} The Prime Number Theorem states:

    limn->oo   P(n) log(n) / n   =    1.

    This says that P(1 000 000)   =~    1 000 000/log(1 000 000)   =   (1 000 000)/(6 log{10)   =~    72 382.

    In other words, approximately 7.2% of the numbers less than 1 000 000 are prime.

  • Are there patterns in prime numbers? Are there formulas for generating them? Is there an efficient way to test whether a given number is prime?

Diophantine Equations: A Pythagorean triple is a triple of integers (a,b,c) so that a2+b2=c2.For example: 32 + 42 = 52. Such numbers are called Pythagorean because they form the sides of a right-angle triangle. Such triples are quite hard to construct.

The equation a2+b2=c2 (with the stipulation that a,b,c be integers) is an example of a Diophantine Equation. Such equations are very hard to solve. Another famous Diophantine equation is the Fermat Equation:

an+bn   =  cn.

Fermat's famous Last Theorem says this equation has no nontrivial solutions for n > 2.

Modular arithmetic is the arithmetic of 12 hour clocks, 7 day weeks, etc., and is fundamental to the theory of groups and rings. We will develop the basic theory of congruence relations. We will then look into congruence equations, focusing on such topics as:

  • Fermat's Little Theorem and Wilson's Theorem.
  • The Chinese Remainder Theorem, which solves systems of linear congruence equations.
  • Quadratic congruences and the Quadratic Reciprocity theorem.
  • Lucas' theorem, which describes the binomial ceofficients, mod p, and has applications to cellular automata.

The Euclidean algorithm is a method to compute the greatest common divisor of two numbers.
MATH-COIS 3210H[321H] Mathematical Cryptography Winter 2009

Description: Cryptography is an area of large and growing importance in modern communication networks, especially in areas of computer security and electronic commerce. Knowledge of this cryptography is thus important to computer science or math students who wish to develop marketable skills for employment in industry. Mathematical cryptography is also an important area of contemporary mathematical research (it is the major application area of modern number theory), and is relevant to any student entering graduate studies in Pure Mathematics or Theoretical Computer Science.

Many encryption systems are based on number theory; the difficulty in breaking these encryption schemes is essentially the difficulty of solving certain hard number theory problems. For example, the RSA public-key cryptosystem is based on the problem of prime factorization (so an efficient factorization algorithm would break RSA encryption). Because of this, advanced number theory is relevant both for breaking existing cryptosystems, and designing new ones which are provably resistant to attack. We will discuss applications of number theory to cryptography, including the RSA and el Gamal public key cryptosystems, and the computational problems of efficiently generating large primes and finding prime factorizations.

Rough Syllabus:

  • Introduction to cryptography: Basic terminology (`plaintext', `ciphertext', `cryptosystem', `key'. etc.) Kerkhoff's principle. `Hard' vs. `easy' computational problems (big `O' estimates of computational complexity). Public-key vs. private key cyptography.

  • Classical Cryptosystems: Shift ciphers. Substitution ciphers. affine ciphers, Vigenère cipher.

  • Shannon's Theory: Information theory. Perfect secrecy. Unicity distance.

  • Modular Arithmetic: The ring structure of Zm. Solution of linear congruences. Fermat's little theorem. Euler's theorem.

  • Modular Arithmetic: The Chinese Remainder Theorem. Key-splitting protocols using the Chinese Remainder Theorem.

  • The RSA cryptosystem: Definition and examples. Vulnerabilities. Weiner's `low decryption exponent' attack.

  • The El-Gamal Cryptosystem: The group of units of Zm; Cyclic groups and primitive roots. The discrete logarithm problem.

  • The Rabin cryptosystem: Solutions to quadratic congruences using Chinese Remainder Theorem.

  • Quadratic Residues: Legendre symbols; Euler's criterion.

  • Quadratic Residues: Gauss's Lemma. Quadratic Reciprocity. Jacobi symbols and generalized quadratic reciprocity.

  • Probabilistic Primality Testing: Background on `Monte Carlo' algorithms. The Solovay-Strassen test and Euler pseudoprimes. The Miller-Rabin test and `strong' pseudoprimes.

  • Factoring algorithms: Background on `Las Vegas' algorithms. Pollard's `(p-1)' and `ρ' algorithms. Dixon's Random Squares algorithm.

  • Discrete Logarithm Algorithms: Shanks, Pollard, Pohlig-Hellmann.

  • (time permitting) Finite fields and Elliptic Curve cryptosystems. Review.


Math 322 Number Theory Discontinued

This course has been split into MATH 3200H[320H] and MATH-COIS 3210H[321H] .

MATH 3260H[326H] Geometry II: Projective & non-Euclidean geometries Not offered 2008-2009

 Elements of projective and non-Euclidean geometries, including an introduction to axiomatic systems.

  • Prerequisite: MATH 1350H[135H] or permission of the instructor.
  • Meetings: Two lectures and one tutorial weekly.
  • Timetable: Not offered
  • Instructor: Not offered
Math 330 Abstract Algebra Discontinued

This course has been split into MATH 3320H[332H] and MATH 3360H[336H] .

MATH 3320H[332H] Groups and Symmetry
(formerly the first half of Math 330) 		Not offered 2008

Groups encode the symmetries other objects. For example:

  • Dihedral groups describe the symmetries of figures in the plane.
  • Polyhedral groups describe the symmetries of polyhedra in three dimensions.
  • Tiling groups describe the symmetries of infinite tilings of the plane.
  • Linear Groups describe symmetries of objects in Euclidean space of many dimensions.
  • Lie Groups describe the symmetries of curves, surfaces, and other manifolds.

Groups can also be thought of as `abstract spaces', or used to encode geometric/topological information. For example

  • Vector spaces are groups with an explicitly spatial structure.
  • Linear groups are groups of linear transformations (i.e. invertible matrices); they encode symmetries of Euclidean space. Thus, group theory is highly relevant to Advanced Linear Algebra (MATH 4350H[435H] ).
  • Galois groups are the symmetry groups for the roots of a polynomial in the complex plane. The structure of these groups encodes important information about the solvability of polynomial equations; this is the starting point of Galois Theory (MATH 4310H[431H] ).
  • Homotopy groups and (co)homology groups describe how curves and other geometric objects can be continously deformed within a surface or other space. These groups encode information about the global topology of the space. This insight leads to a vast and important area of modern mathematical research called Algebraic Topology (MATH 4330H[433H] ).
  • Holonomy groups describe the distortions introduced by traveling through curved space. Thus, group theory arises naturally with differential geometry (MATH 3720H[302H] ).

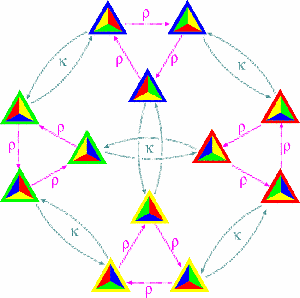
The group of symmetries of a tetrahedron

MATH 3360H[336H] Rings and fields
(formerly the second half of Math 330) 		Fall 2008

Rings are algebraic structures which encode abstract arithmetic.

  • Number rings extend the arithmetic of integers. Many problems in number theory (eg. Fermat's Last Theorem) can be better understood by contextualizing them within ring theory. Thus, ring theory is highly relevant to modern Number Theory (MATH 3200H[320H] ). and Mathematical Cryptography (MATH-COIS 3210H[321H] ).
  • Coordinate rings describe the geometry of a curve, surface, or other space. Many geometric questions about the space can be translated into algebraic questions about the ring, and answered using algebraic methods. This insight leads to a vast and important area of modern mathematical research called Algebraic Geometry (MATH 4370H[437H] ).
  • Group rings provide a natural way to `embed' any group within a ring structure. Matrix rings are (noncommutative) rings of matrices under standard matrix multiplication and componentwise addition. Any homomorphism of an abstract group into a matrix group induces a homomorphism of a group ring into a matrix ring; thus, matrix rings are of central importance in Group Representation theory, which is studied in (MATH 4350H[435H] ).
  • Operator Algebras: are rings of matrices acting on a vector space. They arises in areas from dynamical systems to quantum theory.

A field is a special kind of ring with a particularly rich algebraic structure. The rational numbers, the real numbers, and the complex numbers are examples of fields. Field theory reveals important limitations to mathematical methods. For example:

  • You cannot trisect an angle, double a cube, or construct a 7-gon using a compass and straightedge. It's not that we haven't figured it out yet; it impossible to do these things with only a a compass and straightedge, and this can be proved using field theory.
  • However, there are certain geometric constructions which are possible with origami (i.e. paper-folding) which are not possible with compass and straightedge. (In particular, origami can trisect angles and double cubes).
  • You can solve any quadratic equation ax2 + bx + c=0 with the Quadratic Formula. However, there is no analogous quintic formula for solving a quintic equation ax5 + bx4 + cx3 + dx2 + ex + f=0. It's not that we haven't found it yet; there simply isn't one. This is one of the surprising results of Galois Theory (MATH 4310H[431H] ).

Field theory is also crucial to modern algebraic geometry (Math 437H). Algebraic geometry originally developed as the study of algebraic varieties (curves and surfaces) defined by polynomials over the field of complex numbers. However, many of the key ideas of algebraic geometry can be extended to abstract fields such as the p-adic numbers, which leads to important insights in modern number theory (e.g. the proof of Fermat's Last Theorem).

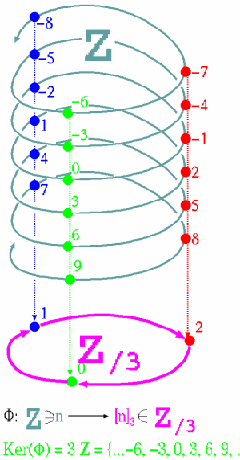
A ring epimorphism from Z into Z/3

MATH-COIS 3350HLinear Programming Fall 2008

Introduction to the concepts, techniques and applications of linear programming and discrete optimization, Topics include the simplex method, duality, game theory and integer programming.

Math-COSC 341 Linear and discrete optimization Discontinued

This course has been replaced with MATH-COIS 3350H[335H] , MATH 3510H[351H] , and or MATH 3610H[361H] .

Math 3510HMathematical finance Not offered 2008

Introduction to mathematical theory and computational techniques for pricing financial derivative contracts: forwards, futures and options. Topics include: hedging and risk management, arbitrage, European and American options, bonds and interest rate derivatives, stochastic calculus, binomial and Black-Scholes models, numerical methods.

Math 355 An introduction to statistical analysis Discontinued

This course has been replaced with MATH 2560H[256H] in the fall semester, and with either MATH 3560H[356H] or MATH 3570H[357H] during the winter semester.


Math 3560HLinear Statistical Models Winter 2009

Linear regression and correlation, multiple regression, analysis of variance and experimental designs. Assumes a background in probability and uses introductory linear algebra.

Math 3570HIntroduction to Stochastic Processes Not offered 2008

This course covers a variety of important models used in modeling of random events that evolve in time. These include Markov chains (both discrete and continuous), Poisson processes and queues. The rich diversity of applications of the subject is illustrated through varied examples.

MATH 3610H[361H] Discrete optimization Fall2008

Introduction to the concepts, techniques and applications of discrete optimization. Topics include transportation problems, assignment problems, matchings in graphs, network flow theory and combinatorial optimization.

MATH 3700H[310H] Metric Geometry and Topology Winter 2009

  Many structures in mathematics seem to possess some kind of `spatial' structure. For example, we often want to say that some sequence of objects converges to some limit object in some sense, or we want to say that a certain transformation is continuous. We often speak of a space of objects satisfying some property (e.g. the space of solutions of an equation). We often want to say that two such spaces are essentially the same; i.e. that one of them is just a `distorted' version of the other one.

Philosophically, we might ask the question, ``What is the essential mathematical structure which all these `spaces' have in common?'' At a more practical level, we might ask, ``Can we develop a general mathematical theory of convergence and continuity, which applies in every situation where these questions arise?'' To answer these questions, early twentieth century mathematicians introduced metric spaces and topological spaces.

A metric space is a set equipped with a way to measure the ``distance'' between any two points. Ordinary Euclidean space and its subsets (such as curves, surfaces, and fractals) are simple examples of metric spaces. More exotic examples include infinite-dimensional spaces of functions, such L2 space (which is of fundamental importance in Fourier analysis, partial differential equations, and quantum mechanics) and zero-dimensional spaces like Cantor space (which is important in the study of fractals and symbolic dynamical systems) or the p-adic number system (which is important in ring theory and number theory).


The Chinese Box Theorem says: if A1 > A2 > A3 > .... is a descending sequence of compact sets, then their common intersection is nonempty. This implies that every contraction mapping on a compact space has a fixed point.

It is easy to generalize to metric spaces the familiar topological concepts of Euclidean space, such as like open sets, closed sets, convergent sequences, continuous functions and compactness, which perhaps you previously encountered in MATH 1100[110] , MATH 2110H[201H] , or MATH 3790H[309H] . We can then prove generalized versions of key results like the Bolzano-Weierstrass Theorem and the Heine-Borel Theorem, and also powerful new results like the Baire Category Theorem. One key application of this theory is the Contraction Mapping Theorem, which can be used to find fixed points of dynamical systems and to identify solutions to many important differential equations.

A topological space does not have a concept of `distance', but still has a structure which encodes the concept of `convergence'. This is important because many natural and important spatial structures cannot be represented using a metric. For example, the most `natural' kind of convergence for a sequence of functions is pointwise convergence, but pointwise convergence cannot be represented using a metric. Also, in algebraic geometry (MATH 4370H[437H] ), the Zariski topology is important for studying the geometry of algebraic varieties.

Another important concept in topology is that of connectedness and the closely related notion of homotopy. A space is connected if it cannot be split into two `separate pieces'. Two spaces are homotopic if one is just a `deformed' version of the other. These concepts form the foundations for an important area of mathematics called algebraic topology (MATH 4330H[433H] ), which studies the `global' properties of topological spaces using group theory.


MATH 3720H[302H] Differential Geometry Not offered 2008

Description:

  Differential geometry was developed in the 19th century (mainly by Carl Friedrich Gauss and Bernhard Riemann) to study the geometry of smooth curves and surfaces in 3-dimensional space, using the methods of multivariate calculus. Indeed, the ideas and methods you learn in MATH 2120H[202H] are all special cases of this more general theory.

  A differentiable manifold is a topological space which generalizes the intuitive notion of a curve or surface. Intuitively, an n-dimensional manifold is a self-contained `universe' which locally `looks like' Rn. This means that we can study the geometry of a manifold near any point by `approximating' the manifold with a vector space (called a tangent space) near that point. Likewise, if f:M --> N is a function between two manifolds, we can study the geometry of f by approximating f with a linear function between their tangent spaces. This linear approximation is called the derivative of f; if f can be adequately approximated in this way, then f is called differentiable. For example, the Euclidean space Rn is a differentiable manifold, and a function f:Rm --> Rn is differentiable in the aformentioned sense if and only if it is differentiable in the sense you learned in multivariate calculus.

  Differential geometry is the study of differentiable manifolds and the differentiable functions between them. It is thus a vast and powerful generalization of multivariate differential calculus, which can be applied to abstract multidimensional spaces. Differential geometry is beautiful for its own sake, but is also of critical importance to other areas of mathematics, including the qualitative theory of ordinary differential equations (also known as ``smooth dynamical systems theory'') and modern mathematical physics (in particular, Einstein's General Theory of Relativity and all of its descendants). Differential geometry is a key area of contemporary mathematical research, and is highly relevant to any student entering graduate studies in pure mathematics, applied mathematics, or mathematical physics.

While concentrating on the classical differential geometry of curves and surfaces in 3-dimensional space, this course will also develop the intuitions and concepts necessary to understand the geometry of abstract manifolds. The philosophy of differential geometry is to study smooth objects through linear approximations; hence the curriculum also includes advanced linear algebra such as multilinear functions and tensor calculus.

Rough Syllabus:

  • Calculus in Euclidean Space; Tangent Vectors. Vector Fields; Directional derivatives. Curves in R3.
  • Linear 1-forms. Differential Forms. Smooth mappings.
  • Dot products; orthogonal frames. Curves. The Frenet Formulas.
  • The Frenet Formulas. Covariant Derivatives. Surfaces in R3.
  • Patch Computations. Differentiable functions. Tangent vectors.
  • Differential forms on surfaces. Smooth Mappings.
  • Integration of Forms; Stokes' Theorem. Topological Properties of surfaces.
  • Differentiable manifolds. The shape operator of a surface.
  • Normal curvature. Gaussian & Mean Curvature. Computational techniques.
  • Special curves in a surface. Frame fields; Connection 1-forms
  • Cartan structure equations. The Fundamental Equations. Form computations. Local Isometries.
  • Theorema Egregium.
  • Time permitting: Introduction to (pseudo)Riemannian geometry, Einstein manifolds, Simplectic geometry, and/or Hamiltonian manifolds.

MATH 3770H[307H] Analysis II: Complex Analysis
(formerly Math 306H) 		Fall 2008

`Complex' analysis should really be called `simple' analysis because of its incredible beauty and elegance. Those who study complex analysis find themselves suspecting that we were `supposed' to live in a complex universe, but we got stuck in a `real' universe by some terrible cosmic accident. In this course, we will emphasise the geometric interpretation of complex-analytic concepts. We will cover the following topics:

  • Complex arithmetic and the complex plane; geometric interpretation.
  • Complex functions as transformations of the complex plane: polynomials, the exponential map, trigonometric functions.
  • Power series. Radius of convergence. How a complex singularity can affect a real power series.
  • Complex multifunctions: fractional powers and the complex logarithm. Branch points and Riemann surfaces.
  • Complex differentiation: The derivative as `Amplitwist'. Conformal maps. The Cauchy-Riemann Equations.
  • Winding numbers and Hopf's degree theorem. Path homotopy.
  • Complex contour integrals; Cauchy's theorem.
  • The Cauchy Residue formula. Calculus of Residues; Laurent series.
  • The Argument Principle. Darboux' Theorem. Rouché's Theorem. The Fundamental Theorem of Algebra
  • The Maximum Modulus Principle. Liouville's theorem.
  • (Time permitting) Introduction to Möbius transformations and the Riemann sphere.
   
Colour-coding the complex plane in polar coordinates


The complex exponential map, seen through this colour-coding.

MATH 3790H[309H] Analysis I: Introduction to Analysis
(formerly Math 206H) 		Fall 2008

A sequence of successively higher order Taylor polynomials converge to the sine function.

 The real number system. Limits. Continuity. Differentiability. Mean-value theorem. Convergence of sequences and series. Uniform convergence.


Math-Science 380 History of mathematics Discontinued

This course has been split into MATH 3810H[381H] and MATH 3820H[382H] .

Math.-Science 3810H
(The first half of the former Math 380) 		Ancient and Classical Mathematics Not offered 2008

This course traces the historical development of mathematics from prehistory to medieaval times, and the interactions between the development of mathematics and other major trends in human culture and civilization. We will study the mathematics of ancient Egypt and Mesopotamia, and classical Greece and Rome.

Math.-Science 3820H
(The second half of the former Math 380) 		Mathematics from mediaeval to modern times Fall 2008

This course traces the development of mathematical ideas, abstraction and proofs. The genesis of modern arithmetic in mediaeval India, the birth of algebra in the Islamic world, and their influence mediaeval European mathematics. Renaissance mathematics (polynomial equations, analytic geometry). The Enlightenment (calculus, number theory). The apotheosis of rigour since the 19th century.


MATH 3900[390] Reading-seminar course (Full) Fall and Winter (reading course)
Details may be obtained by consulting the Department of Mathematics.

MATH 3901H[391H] Reading-seminar course (Half) Fall or Winter (reading course)
Details may be obtained by consulting the Department of Mathematics.


MATH 3902H[392H] Reading-seminar course (Half) Fall or Winter (reading course)
Details may be obtained by consulting the Department of Mathematics.


MATH 3903H[393H] Reading-seminar course (Half) Fall or Winter (reading course)
Details may be obtained by consulting the Department of Mathematics.


MATH 3904H[394H] Reading-seminar course (Half) Fall or Winter (reading course)
Details may be obtained by consulting the Department of Mathematics.


1000-Level ....... 2000-Level ....... 3000-Level ....... 4000-Level

Math logo
Department of
Mathematics
Index of math courses
Dependency lattice for pure math courses (PDF)
Dependency lattice for applied math courses (PDF)
Math Course Classification Grid (PDF)
Math program requirements
Student Handbook
Enjoying Math!
Fall 2008 Mathematics Course Timetable
Winter 2009 Mathematics Course Timetable
Trent crest
Trent University


This page maintained by Marcus Pivato.
Last updated 2008-03-21