| 1000-Level | ....... | 2000-Level | ....... | 3000-Level | ....... | 4000-Level |
This course has been replaced with MATH 2110H[201H] and MATH 2120H[202H]
This course has been renamed as MATH 3790H[309H]
This course has been renamed as MATH-COIS 2180H[203H]
A course in mathematics and mathematical thinking for prospective school teachers. Number systems and counting, graphs and networks, probability and statistics, measurement and growth, symmetry, computers and mathematics. Not available to students enrolled in or with credit for any of Math 1100[110] , MATH 1350H[135H] or MATH-COIS 2600H[260H] or their equivalents. Not for credit towards any major in Mathematics.
- Note: Instructor's approval required; enrolment limited.
- Meetings: Three-hour lecture/workshop weekly.
- Timetables
- Section A: Full Year
- Section B: Not offered
- Section C: Not offered
- Instructor:
- Section A: Grad T.A.s
- Section B: Not offered
- Section C: Not offered
- For more information, please see the (old)Math 2080 homepage.
Description: This is a general-interest course about topics in mathematics that are studied for fun. These topics include magic squares, logic puzzles, toys and tricks with mathematical content, polygonal dissections and tiling problems, etc. These topics will be especially interesting for anyone who wants to become a math teacher, and will also appeal to non-mathematicians who have a casual interest in math (e.g. geometric puzzle aficionados, readers of Martin Gardner's ``Mathematical Games'' and similar columns in Scientific American, etc.). Some possible topics include:
- Magic squares
- History.
- Algorithms for generating magic squares.
- Tricks for modifying magic squares to create new ones.
- Magic squares with additional properties.
- Logic problems and puzzles
- Deductions involving logical alternatives.
- Puzzles and paradoxes involving self-references, including:
- The lady or the tiger.
- The unexpected hanging.
- Dissections
- Cutting up polygons into pieces and reassembling them into other polygons.
- When can a polygon be dissected into another polygon?
- What happens with non-polygonal shapes?
- What happens if pieces are ``cut'' in more complex ways?
- Tilings
- What combinations of tiles can be used to cover a floor?
- Periodic and non-periodic tilings.
- Connections between dissections and tilings.
- Polyominoes
- What shapes can be created with given sets of polyominoes?
- Tilings using polyominoes.
- Reptiles (polyominoes which can be tiled by smaller copies of themselves).
- Extensions of polyominoes to three dimensions, e.g. the Soma cube.
- Map colouring
- The general Four-Colour Theorem.
- The Two-Colour Theorem for a map created by drawing (possibly overlapping) circles. Investigate how far this theorem can be extended.
- Arithmetic tricks
- Puzzles based on tables for arithmetic operations.
- Divisibility tests and why they work.
- Conway's Game of Life
- Stable, periodic, and moving patterns in the Game of Life.
- ``Garden of Eden'' patterns.
- Computing using the Game of Life and other cellular automata.
- Arrangements
- Kirkman Schoolgirl Problem and Steiner systems.
- Small finite affine and projective geometries.
- Applications to puzzles, experimental design, and coding.
- Prerequisite: Any Grade 12 Mathematics credit or equivalent; and two full credits in any subject(s) at the 100 level, or permission of the instructor.
Not for credit towards a major in mathematics.
- Meetings: Three lectures and one tutorial weekly.
- For more information, please see the MATH 2084H homepage.
- Winter Class timetable .
- Instructors: Stefan Bilaniuk.
Description: This is a general interest, interdisciplinary course exploring the interactions between mathematics and the arts. Its goal is to introduce students (with or without prior mathematical experience) to the beauty of mathematics, and show how mathematical concepts can help elucidate aesthetic principles. Possible topics include:
- Symmetry:
- The 5 regular (`Platonic') polyhedra and 13 semiregular (`Archimedean') polyhedra.
- Frieze groups, with applications to canons and fugues (especially J.S. Bach).
- Planar tilings and crystallographic groups. Medieval Islamic art and the tilings of M.C. Escher.
- Self-similarity and Fractals:
- Fractal geometry in natural forms (e.g. trees, snowflakes, mountains, coastlines).
- Fractals and multiscale self-similarity in art (e.g. 19th century Japanese woodcuts) and music (e.g. Balinese Gamelan music and Colin McPhee, or J.S. Bach's canons).
- The golden ratio: Fibonacci numbers, golden rectangles, golden spirals, importance in classical and Renaissance art.
- Musical Harmony:
- Musical notes as frequencies; an octave as a frequency doubling. Harmony as low-denominator frequency ratios.
- The circle of fifths
- Harmonics and chords.
- Well-tempered tuning and base-2 logarithms.
- Modular arithmetic as a model of cyclical time. Applications to musical rhythm patterns.
- Self-reference:
- Induction and recursion in mathematics.
- Self-referential structures and metamathematics. Gödel's Incompleteness Theorem.
- Self-reference and postmodernism in art and literature.
- Mathematics in architecture: the Parthenon; Renaissance military engineering; mazes and labyrinths.
- Art inspired by mathematics. For example:
- Mathematically themed visual art and sculpture (e.g. M.C. Escher, Sol Lewitt).
- Mathematically inspired music (e.g. Iannis Xenakis).
- Mathematically inspired literature. For example:
- Rudy Rucker's White light.
- Douglas Hofstadter's Gödel, Escher, Bach.
- Michael Crichton's Jurassic Park.
- The short fiction of Jorge Luis Borges, e.g. ``The Library of Babel'' or ``The Immortal''.
- The short ficton of Greg Egan, e.g. ``Wang's Carpets'' or ``Unstable Orbits in the Space of Lies''.
- Alex Kasman's Reality Conditions.
- Clifton Fadiman's Fantasia Mathematica.
- William Frucht's Imaginary Numbers.
- Mathematics in drama (e.g. David Auburn's Proof, Tom Stoppard's Arcadia, Michael Frayn's Copenhagen, John Mighton).
- Mathematics in television and cinema (e.g. Pi and Numb3rs).
- Prerequisite:
Any Grade 12 Mathematics credit or
equivalent; and two full credits in any subject(s) at the 100 level,
or permission of the instructor.
Recommended pre/corequisites: MATH 2260H[226H] , or CUST 211 (Drawing) or CUST 216 ( Introduction to Visual Studies) or CUST-ENGL 229 (Science Fiction) or CUST 245 (Music and Society).
These recommendations are for student interest only; they are not required.
-
Not for credit towards a major in mathematics.
- Meetings: Three lectures and one tutorial weekly.
- For more information, please see the MATH 2085H homepage.
- Not offered Class timetable.
- Instructors: Not offered
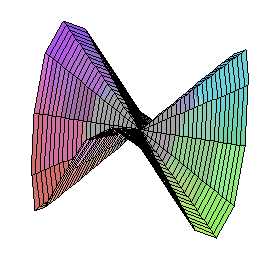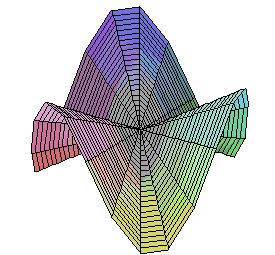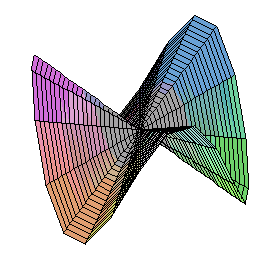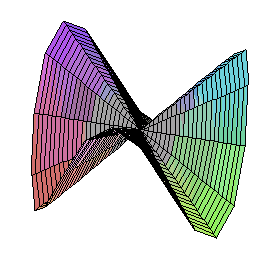 The Monkey's Saddle is not differentiable at zero, but all tangent lines exist there. |
Multivariable functions, curves and surfaces in two and three dimensions. Partial differentiation and applications. Multiple integrals.
|
Parametric curves and surfaces, vector functions and fields. Line integrals, Green's Theorem. Surface integrals, curl and divergence, Stokes' and Divergence Theorems.
- Prerequisite: MATH 2110H[201H] .
- Class timetable
- Instructor: Marcus Pivato
Synopsis:: First order equations; qualitative and numerical methods. Second order linear equations. Applications to physical and biological models. Laplace transforms. Power series solutions. |
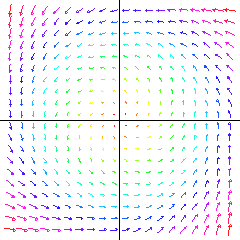 A two-dimensional vector field determines a flow in the plane. |
|
Overview: Ordinary differential equations (ODEs) model physical systems which evolve continuously in time. For example, suppose the state of the system is described by a single variable , and satisfies the equation:
Suppose the state of the system at time is given by a real vector in . Then an ODE for this system has the form:
|
ODEs are ubiquitous in applied mathematics. For example:
Given an ODE, we can ask four questions:
|
(formerly Math 207H)
Error analysis, non-linear equations, linear systems, interpolation methods, numerical differentiation and integration and initial value problems.
- Prerequisite: MATH 1005H[105H] or MATH 1100[110] .
- Meetings: Three lectures and one tutorial weekly.
- For more information, please see the MATH 2180H homepage or the last year's MATH 2180H homepage.
- Class timetable
- Instructors: [To Be Announced]
This course is intended for mathematics majors in the first or second year of their program, and introduces the essential concepts, methods, paradigms and abstractions of higher mathematics. It is recommended as a pre/corequisite for upper level pure math courses such as
MATH 3720H[302H] , 307H, 309H, 310H, 320H, 321H, 332H, 336H, 407H, 409H, 410H, 415H, 431H, 432H, 433H, 435H, 437H, 416H, 461H, 462H, 471H, and 472H. We will cover most of the following topics:
- Proofs and logic: Modus ponens; proof by cases; proof by contradiction (eg: Euclid's proof that there are infinitely many prime numbers; Cantor's diagonal argument). Proof by induction (e.g. the Euclidean algorithm; Lamé's theorem.)
- Sets and functions: Sets and subsets; union and intersection; de Morgan's laws. Functions: injective, surjective, and bijective. Inverse images.
- Combinatorics: Counting arguments; the Pigeonhole Principle; factorials, binomial coefficients, Pascal's formula; the binomial theorem. Multinomial coefficients and the multinomial theorem.
- Transfinite Arithmetic: Cantor's definition of cardinality; The sets N, Z, N2, and Q all have cardinality Aleph0. Cantor's diagonal argument, showing that R has cardinality c > Aleph0.
- Complex numbers: The complex plane in Cartesian and polar coordinates. Addition, multiplication, and the exponential map, and their geometric interpretations. de Moivre's formulae.
- Basic Number Theory:
- Divisibility; greatest common divisors, lowest common multiples. The Euclidean algorithm. Fibonacci numbers and Lamé's theorem.
- Linear diophantine equations. Brahmagupta's theorem.
- Prime numbers and prime factorization. The Fundamental Theorem of Arithmetic.
- Modular arithmetic: Modular addition and multiplication; the concept of equivalence class, with congruence classes as the prototypical example. Linear congruence equations. Fermat's little theorem.
- Possible additional topics: We may have time for one or two of the following topics:
- Symmetry and Transformation groups: Symmetries of plane figures. Transformation groups. Examples: dihedral group, matrix groups, permutation groups. Subgroups, group homomorphisms and group isomorphisms.
- Introduction to topology: Curves, surfaces, and manifolds. Homeomorphism and homotopy. The Euler-Poincaré invariant and the fundamental group.
- Prerequisite or Corequisite: MATH 1100[110] and MATH 1350H[135H] .
- Meetings: Three lectures and one seminar weekly.
- Class timetable
- Instructor: David Poole
- For more information, please see the MATH 2200H homepage.
Geometry is the oldest part of mathematics; its origins are lost in antiquity. Classical Euclidean geometry applies logical deduction to discover the relationships of lines, points, and circles in the plane. For more than two thousand years, it has been the ideal of clarity and elegance to which all other mathematics aspires. In this course, we will cover some subset of the following topics:
|
A construction of a pentagon using only compass and straightedge.
|
Recommended for Education students.
- Prerequisite: Either MATH 1005H[105H] or MATH 1100[110] (with OAC Algebra/Geometry recommended), or 135H.
- Meetings: Two lectures and one tutorial weekly.
- Class timetable
- Instructor: David Poole
Vector spaces, basis and dimension, inner product spaces, orthogonality, linear transformations, diagonalization, determinants, eigenvalues, quadratic forms, least squares, the singular value decomposition.
- Prerequisite: MATH 1350H[135H] .
- Meetings: Three hours lecture and one hour tutorial weekly.
- Class timetable
- Instructor: Stefan Bilaniuk
(formerly the first half of Math 355)
Introduction to mathematical statistics: Methods of point estimation, confidence intervals, hypotheses testing, comparative inferences, nonparametric methods.
- Prerequisite: MATH 1550H[155H] . Also ssumes a background in probability and calculus.
- Meetings: Three hours lecture and one hour tutorial weekly.
- Class timetable
- Instructor: Michelle Boue
Mathematics related to computer science including propositional logic, recursive functions, combinatorics, graphs and networks, Boolean algebras. Applications to languages, analysis of algorithms, optimization problems, coding theory, and circuit design.
- Prerequisite: MATH 1100[110] or MATH 1350H[135H] ; or COIS 102H together with one Grade 12 U or U/C or OAC credit in Mathematics.
- Recommended: OAC Finite Mathematics.
- Meetings: Three hours weekly.
- Class timetable
- Instructor: David Poole
- For more information, please see the MATH 2600H homepage.
| 1000-Level | ....... | 2000-Level | ....... | 3000-Level | ....... | 4000-Level |

