Interactive Web-Based Mathematics Communication

by Marco Pollanen

About the Author: Marco Pollanen is an Assistant Professor at Trent University.

Subject Classification: 3.1 Algebra, 4.0 Discrete Mathematics, 6.0 Calculus, 9.0 Statistics and Probability, 10.0 Applied Mathematics

Keywords: online communication, symbols, pedagogy, calculus, algebra

Introduction

While the Internet offers phenomenal opportunities for communication, most of the available tools for personal interaction, such as e-mail, chatrooms, instant messaging, and bulletin boards, are "text-based." Many subjects, in particular the mathematical sciences, rely heavily on symbols, visual aids and other non-textual communication, with the result that for mathematics much of the interactive potential of the Internet has thus far not been realized.

For mathematicians communicating with colleagues over the Internet, this is a minor annoyance, as PDF files can be exchanged, and the vast majority of mathematicians can read raw TeX notation, for example \int_0^1 x^2 dx, embedded in e-mail. However, mathematical communication over the Internet with students using text, for example via e-mail, can be a slow and frustrating process. First-year students often have enough trouble with the proper use of parentheses in communicating mathematical concepts. In e-mail format, where expressions must be inline, they tend to write statements like x2+1, 1/2x and sin x + y, all of which are ambiguous. Included in integrands or fractions, and combined with Greek letters and subscripts, these expressions can become incomprehensible.

The problem becomes particularly acute for live interactive communication, where students must produce unambiguous equations and diagrams quickly. Over the past decade the Internet has changed the way mathematics is taught. Many introductory math courses are delivered completely online, and even more are available in hybrid format. Since most theories of education maintain that personal interaction -- whether teacher to student, student to teacher or student to student -- is a cornerstone of learning, this presents a serious challenge for mathematics educators. Many online courses have little live interaction, and allow students to access only course outlines, notes and assignments, post to message boards and send e-mail. The more interactive online courses available today still provide only a text-based chatroom or a whiteboard, which can be inadequate for communication in a visual subject such as mathematics. Furthermore, because these technologies are cumbersome for communicating mathematical content, they tend not to be utilized by a significant portion of students.

In this article I will introduce and discuss my experiences with incorporating into teaching a new technology I have created, called enVision, which aids in communicating mathematical content. While there is significant potential for this software in online courses, in this article I will focus on my experiences with using this technology to hold anonymous online office hours in a traditional course. While office hours are a valuable and unique teaching tool, it is a common observation that students in introductory mathematics courses do not attend them. Many feel confused and intimidated by mathematics and do not want to reveal how little they think they know. This in itself is a communication barrier that impedes learning in mathematics and presents a missed opportunity for both student and instructor. In my experience, enVision has helped make me, as a math educator, more accessible to students, and has helped students reduce or overcome any shyness or math phobia they may have.

The enVision Platform

Overview

The enVision platform consists of two packages, a front end -- the enVision Web interface -- and a back-end server, called MathServer. The enVision interface is what a typical user will see and interact with. It loads into a standard Web browser with no installation, and helps users input and communicate their ideas. It has two communication components: a shared workspace, where any number of participants interact with each other in a mathematical discussion, and a text chat window, where most of the other discussion occurs. The shared work space is essentially a whiteboard drawing program that has special drag-and-drop resizeable math symbols, as well as a panel of special math characters that can be placed with ease onto the whiteboard. Everything that is written on the whiteboard and the chat area is visible to all participants. MathServer is the application that relays the information between different users to ensure that their enVision interfaces are synchronized, thus creating and maintaining a shared workspace.

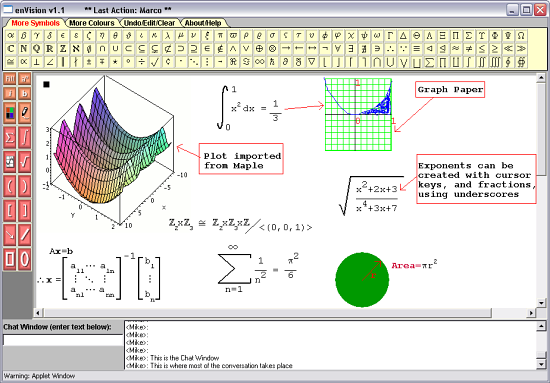
Figure 1: Student Mode view of enVision interface (Internet Explorer browser)

The core philosophy of enVision is simplicity and ease of use, i.e., allowing for the communication of mathematical content as easily and quickly as possible with a minimal learning curve, for both student and instructor, and minimal hardware and software requirements. The emphasis is on communication in a quick and intuitive fashion, rather than having typeset letter-perfect documents.

In order to keep the program platform independent and accessible to low-bandwidth users, enVision supports a core set of functionalities. It makes it possible to load JPEG and GIF images, which could easily be extracted from applications like Maple, or from PDF documents, with freely available programs like ImageMagick. Likewise, it is assumed that if video or audio are desired features, appropriate packages could be loaded simultaneously. Although enVision is easy to install and maintain, it also has advanced features that allow for integration and customization into existing environments such as Blackboard and WebCT. In short, the program can be easily installed and running in minutes as is, but it is also flexible and can be customized by those who are inclined to do so.

enVision Web Interface

Most of the interface options are accessed through the orange/pink button panel on the left-hand side of the interface or the tabbed panels on top of the applet.

Button(s)	Function	Button(s)	Function
	Toggle fill mode on/off for ovals and boxes		Toggle text size (useful for superscripts and subscripts)
	Toggle italics and bold text on/off		Change color (cycling through black, red, green, and blue)
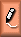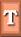	Toggle between sketch and text mode		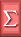Resizeable drag and drop sum, integral and root symbols
	Resizeable drag and drop graph paper		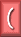Resizeable drag and drop parentheses
	Resizeable drag and drop brackets for matrices		Resizeable drag and drop arrow for pointing
	Line drawing tool		Rectangle and oval drawing tools for drawing both filled and unfilled shapes

Table 1: Functions of the main buttons on the enVision interface

The small orange buttons are essentially toggle switches, which toggle fill mode (for rectangles and ovals), subscript text (on/off), italicized text (on/off), and bold text (on/off).

The first large orange button cycles through four colors (black, red, green, and blue), while the second large orange button toggles text and sketch modes, which is particularly useful if you are on a tablet PC.

The pink buttons are for drawing the following resizable objects: sums, integrals, graph paper, roots, parentheses (left/right), brackets (left/right), arrows, lines, rectangles and ovals.

The tabbed panels assist in editing and provide easy access to additional symbols and colors. Keyboard shortcuts are also described in the edit panel.

One of the key features of enVision is the behavior of the cursor in text mode. The cursor keys move the cursor in half-steps to allow for the easy creation of exponents, subscripts, etc. By clicking the mouse or using the <F1> key, users can set alignment marks for the Enter key to line up text. The Backspace key also acts as an undo key for both text and symbols.

Finally, additional information regarding which user is using the whiteboard component is displayed on the title bar of the enVision window (when the whiteboard is locked, the title bar displays its locked status).

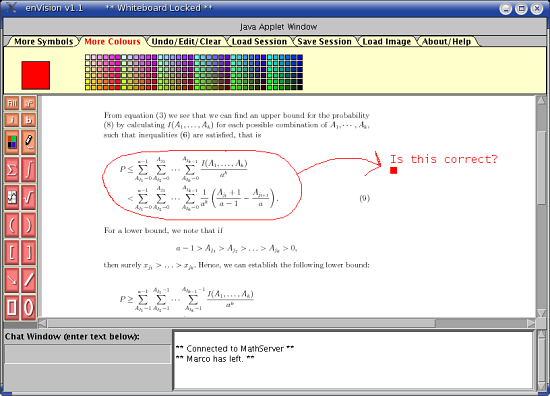
Figure 2: Instructor Mode view of enVision interface displaying PDF (Linux with Firefox browser)

MathServer

MathServer is a simple program that runs on the Web server from which the enVision applet is downloaded. Only the system administrator installing MathServer would have to be concerned with it, as it is invisible to other users. It has two functions: to receive and distribute any content input by enVision users which is then displayed for all users on the whiteboard, and to load and save sessions. MathServer must be running in order for different enVision users to communicate with each other.

Software Specifications

I. enVision Interface

The enVision Web interface is a Java applet which the instructor and the student load by visiting the appropriate pages with their browsers. The applet is designed to be very small, approximately 58KB (about the size of an average web page), so that it can be loaded without delay by large numbers of students simultaneously and by users with dial-up connections. It is designed to be as platform-independent as possible, so it will run on any browser that supports at least Java 1.1, including the outdated Java Virtual Machine shipped with a default Internet Explorer installation. Thus, virtually any student with access to the Internet would be able to use the enVision interface. However, if you download the latest Java plug-in, it will run in virtually any other browser. To date, it has been tested on numerous configurations of Internet Explorer, Netscape, Mozilla Firefox, Safari and Opera, as well as various Windows, Mac, and Linux operating systems, without any major issues arising.

If MathServer is running, the instructor must ensure that the enVision.jar and HTML page(s) that load it are accessible on the Web server. Then, all the instructor has to do to log on is load the appropriate Web page into his/her browser. For students, all that is required is to load the appropriate Web page into their browsers. Note, however, that the instructor can make a number of customizations by changing the applet parameters in the HTML page that loads enVision.

Optional Applet Parameters:

<param name=host value=192.0.2.5>    
<!-- This sets the IP address that enVision will connect to (it is a good idea to set it). -->

<param name=port value=8000>         
<!-- This sets the port to the given value. The default is 8080. -->

<param name=instructor value=true>   
<!-- This sets the applet to instructor mode. The default is student mode. -->

<param name=username value=UserName> 
<!-- This sets the username (useful if you have your own authentication script). -->

<param name=announce value=false>    
<!-- This turns off the log in/out announcements in the Chat Window 
     (especially useful in large classes).-->

Instructor and student modes are similar, although they must be accessed from separate HTML pages. There are, however, several noteworthy differences. Students cannot load and save sessions and images, but the instructor could let students access this mode to load and save sessions after class. Instructors also have the ability to lock the whiteboard, so that no student can write on the board, by using the <F12> key. If this is done, other instructors may still write on the board. In this mode, both students and instructors can still write to the chat window. The locked status is displayed on the title bar. Using the <F12> key when in locked mode would then unlock the whiteboard.

The images that are used in the More Symbols panel are located in the enVision.jar Java Archive as files 0.gif to 119.gif, numbered in the order in which they appear on the panel. The instructor could customize them, so as to use different symbols instead, by replacing the existing GIF file with another.

II. MathServer

MathServer is a platform-independent Java application. It must be running on the Web server from which the user's browser loads the enVision applet. To start MathServer, the instructor must have permission to run processes on the Web server or have the system administrator start it.

Provided Java is installed on the server, MathServer is started by issuing the command "java -jar MathServer.jar" followed by an optional port number. (The default port is 8080.) Any firewall software running on the Web server must be set to allow access to the port that MathServer is set to listen to. When the enVision applet is loaded and the server is running, "** Connected to MathServer **" should appear in the Chat Window. If it does not appear, there is either a problem with the firewall or the IP/port settings in the applet tags.

If a subdirectory called "files" exists, the server will load and save sessions in that directory using the .mth extension. Note that if you wish to load images (GIF and JPEG formats are supported), they must be located in the directory (or subdirectory) from which the enVision applet was loaded (not the "files" subdirectory).

III. External Applications

As enVision only allows for the loading of images in GIF and JPEG format, one could also consider installing an image conversion tool. As long as the instructor can transfer the resulting images to the Web server, these tools can run on any machine that the instructor has access to. ImageMagick is a free cross-platform utility useful for obtaining and manipulating images for use in enVision from other programs, such as Maple. For example, the command "convert file.pdf[8] file.gif" would extract page 9 (as it assumes pages start from the number 0) of a PDF file and save it as a GIF file, and the command "import file.gif" can be used to create a GIF image from a region of the screen, and thus a screenshot of virtually any application can be loaded into enVision.

Availability

enVision v1.1 is freeware. Its project homepage is http://www.xiom.org, where you can download a copy, try a demo version, and find documentation and updates.

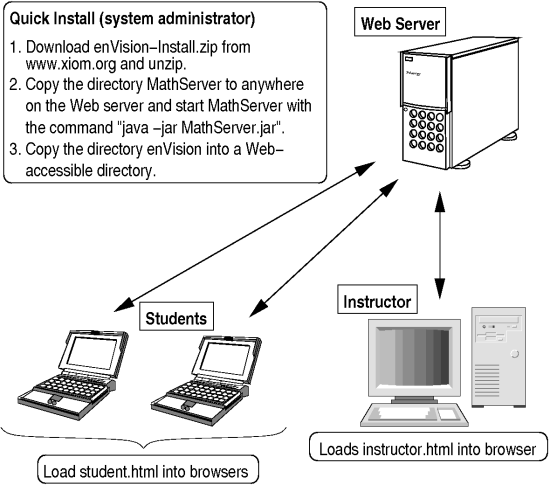
Figure 3: Overview of enVision basic installation

Learning Outcomes

I have used enVision successfully in large and small class settings, at both large and small universities.

I created the first version of enVision in 2000, while I was a teaching assistant at the University of Toronto. I tried to make myself as accessible to students as possible. However, at the time, I taught multiple sections of introductory calculus tutorials, including some in the evenings (students in these sections were often employed full-time during the day) and some at a distant suburban campus (students would have difficulty meeting me downtown at my office). A live online office hour was the best practical option in order for my students and myself to be able to communicate.

More recently, I have been teaching at Trent University, a smaller liberal arts university, and have been using enVision in a second-year discrete mathematics class of about 25 students. As the course is primarily for computer science majors, students generally feel apprehensive about mathematics. Since enVision was originally conceived as a tool for large or multi-section classes, I have only recently started to experiment with it in this course. I currently supplement my regular office hours with one extra online office hour, during which students can log on anonymously (i.e., using any name they wish). The results have been impressive. Communication has improved; at times, up to half the students in the class attend the online office hour simultaneously.

Based on my experiences, anonymous online office hours are advantageous for addressing the following issues:

Overcoming Math Phobia: Math phobia is a widespread problem, especially among non-mathematics majors. A common symptom is extreme mathematical timidity. Only a minority of students ask questions in a math class or come to a traditional office hour. When students are surveyed about the use of enVision, one of their most frequent comments concerns the value of being able to ask questions anonymously.

Greater Participation: Forming opinions, whether correct or incorrect, is an important part of the learning process. Aside from the fact that more students attend online office hours, anonymity leads to more mathematical discussion and allows me to ask students for responses without their fearing that I am singling them out. Students are far more likely to interpolate and add value to online discusions.

Greater Accessibility: Students lead complex lives. Due to conflicting commitments with school, work, and family, and long-distance commutes, many students have difficulty attending regular office hours. I tend to hold online office hours late in the evening, at times when my students are most likely to be studying.

Efficient Use of Time: My online office hours are scheduled only by start time, and thus students tend to be punctual. If there are only a few questions, I log out after answering them, so a significant time commitment is not required on the part of the instructor. Although the interface is not a complete substitute for face-to-face interaction, it does have its advantages. While I wait for students to respond to questions I have posed, I find it convenient to be able to access other instructor resources, such as books, notes, etc., to search for more examples or to plot a Maple diagram for them to consider. Finally, all the sessions can be saved and archived, and so answers to common questions do not have to be repeated and are made available to all my students (and could perhaps be made available to students in future years as well).

Addressing Different Learning Styles: Some students learn by writing things down. However, others learn better by being able to concentrate on the discussion and replay the saved sessions later rather than furiously scribbling what is on a professor's office blackboard during a traditional office hour.

Improved Classroom Atmosphere: I find that another benefit of strengthening dialogue outside the classroom is a more relaxed, open, and encouraging atmosphere in the classroom, as more questions are asked in class as well.

Conclusion

Although interactive Web-based communication is not a substitute for face-to-face interaction, enVision does help facilitate online mathematical discussion. In particular, as today's students tend to be relaxed and comfortable with e-mail and instant messaging, they seem to be open to online office hours, and holding virtual office hours seems to have a number of pedagogical benefits when appropriate communication tools are available. This technology could also be used to encourage more dialogue between students in a student-helping-student model of learning, especially in a completely Web-based course.

Resources

Links

enVision Project Homepage--Documentation, updates and live demos of enVision can be obtained here.
ImageMagick Project Homepage--ImageMagick is a free cross-platform utility useful for obtaining and manipulating images for use in enVision from other programs like Maple.