A Quick Guide to Shang for Matlab Users

Xiaorang Li

Shang is designed to be a general programming language that is strong in numerical computing. The numerical matrix facilities and control structures of Shang are very similar to that of Matlab. If you are familiar with Matlab, you probably can start use Shang right away. However, Shang design follows a cleaner, more orthodox approach, with many powerful new features. There are still quite a number of differences between the two. Here is a list of some of the most important things someone familiar with Matlab may want to know.

Syntax and General

1. Comment

   Two slashes // start a comment line. A matched pair of /* and */ enclose multiple lines of comments.

   The percent sign % is used as the mod operator.

2. Space is not a separator

   Shang is more strict on free-form syntax and doesn't allow using space or newline as separators. When a matrix is created using bracket expression, elements must be separated by comma or semicolon. For example, A = [3, 5, -1; 2, -7, 9]. In particular, A = [3 5 -1; 2 -7 9] would result in syntax error, while A = [5 -1; 2 -7] gives A = [4, -5].

3. No distinction between ``function file'' and ``script file''

   There is no ``function file''; every program file is a ``script'' file. A script file can contain any number of function definitions.

4. No automatical loading of program files

   Interpreter does not load script files automatically. To run the commands in a file prog.x, one has to do run(``prog.x'') or with(``prog.x''). The command with loads the program only if it's the first time it is called, or the file has been updated.

Matrix

1. k-th element of A is A[k]

   The matrix indexing operator is []. For example, the second element of x is x[2] and the element of A at row 3 and column 5 is A[3,5].

2. A(x) means A * x

   A(x) is evaluated as A * x. That is, matrix A is used as a linear function (In order for A(x) to work, the number of rows of x should match the number of columns of A). A matrix is a function and can be used anywhere a function is expected.

3. Row major storage format

   Dense matrices are stored in row major order. Thus, if A is an $m\times n$ matrix, A[j, k] is equivalent to A[j * n + k].

4. The last element of A is A[$]

   The last element of A is A[$], not A[end].

   The last element on the third row of A is A[3, $], not A[3, end].

5. rand(n) is the same as rand(n, 1) not rand(n, n)

   rand(n), zeros(n), and ones(n) return $n\times 1$ matrices in stead of $n\times n$ square matrices. To obtain square matrices, one has to use calls like rand(n, n)

6. Matrix Storage Format

   Dense matrices are stored in row major order, as opposed to the column major order used in Matlab. This means that each row of a matrix is usually stored in a contiguous memory block, and the rows are stored one after another.

   Row major and column major are equivalent when elements of A are accessed by using two indices like in A[i, j]. However, expression with a single index behaves differently in row major and column major. For example, if A is a matrix of 5 rows and 5 columns, then A[1], ...,A[5] are the five elements in the first row, while A[6], ..., A[10] refer to the five elements in the second row.

7. More powerful Indexing Expressions

   Semicolons and backslashes can be used in indexing expressions. For examples

   • A[1, 2, 3; 4, 5, 6] extracts a vector [A[1,3], A[2,4], A[3,6]].
   • A[\] extracts the diagonal of A.
   • A[\,1] extracts the first super diagonal of A, A[\,-2] extracts the second sub diagonal of A, and A[\,0:n-1] extracts the upper triangle of A.

   • A[\] = 1 sets the diagonal values of A to 1.

Function

1. Functions are ``nameless''; no need for feval

   A function is a value, which can be assigned to a variable, stored in a list, passed to a function, or created and returned by another function. A function does not need a ``handle'' -- it can handle itself just fine. The following is an example of a function definition

       function n -> s
          s = 0;
          for k = 1 : n
              s += 1 / k^2;
          end
       end
   

   Note that the function keyword must be matched by an end. Functions are ``nameless''. To be able to call a function, it should be assigned to a variable. For example

       h = function n -> s
          s = 0;
          for k = 1 : n
              s += 1 / k^2;
          end
       end
   

   Now to call the function with argument value n=1000, one can do h(10000).

   If a function definition just contains a single statement, then the function and end keyword are not necessary. For example, f = (x, y) -> (x+y) / (x^ 2+y^ 2+1) defines the function $f(x,y)=\frac{x+y}{x^2+y^2+1}$.

   A function definition is no more special than assigning a constant value to a variable. Therefore, a program can contain as many function definitions as needed; function definitions can contain function definitions and can return function definitions, etc.

   There is no need for feval. When you pass a function value to another function, just pass it, there is no need to play with strings, ``function handle''s or feval.

2. Polynomial

   Polynomial is implemented as a built-in function poly. It has a public parameter coeff. No polyeval is necessary as a polynomial is already a function and can be called directly. For example

      >> p = poly;               // make a copy of the built-in function poly, now p(x) = 1;
      >> p.coeff = [3, -2, 1];   // update the coefficient, now p(x) = 3 - 2x + x^2
      >> p(10)                   // evaluate the polynomial
           83
      >> int(p, [0, 2])          // integrate p(x) from 0 to 2
           4.666666667
   

   Or a new polynomial can be spawned by provided the values of the parameters

      >> p = poly[[3, -2, 1]];   // spawn a new polymial by given the value of the
                                 // only public parameter
      >> p(10)                   // evaluate the polynomial
           83
      >> int(p, [0, 2])          // integrate p(x) from 0 to 2
           4.666666667
   

3. Functions can be added, multiplied, etc

   E.g., sin - cos defines a function $f(x) = \sin x - \cos x$.

4. No nargin or nargout

   There are no ``nargin'' and ``nargout'' inside a function body to tell the number of input and output arguments.

5. Default argument value

   The default argument value is specified in the function definition header. For example

   f = (x, alpha = 1) -> sqrt(x^2 + alpha^2);
   

   Then f(x) is equivalent to f(x, 1) since the argument alpha receives the default value.

   If no default value is specified, the argument will receive null when no value is passed to it. For example, here f() is equivalent to f([], 1), as both arguments now receive default values.

   The symbol * is equivalent to default value. So in function call f(*, 2), the first argument receives the default value and the second receives 2.

6. Variable number of arguments

   If a function expects one argument value but receives more than one, then those values are made a list and passed to the function as a whole. For example

   f = function args -> v
       ...
   end
   

   Then when f is called by f(x, y, z, w), args receives the list (x,y,z,w).

   On the other hand, if f expects a bunch of argument values, but passed one list, then the entries of the list will be retrieved and passed to those arguments. For example

   f = function (x, y, z, w) -> v
       ...
   end
   

   Then

   args = (a, b, c, d);
   f(args)
   

   is equivalent to f(a,b,c,d).

7. Multiple return values

   A function that has multiple return values always returns a list of those return values, regardless of how many values the function call is assigned to.

   For example,

   f = function (x, y) -> (z, w)
       // function definition --- should assign values to z and w
   end
   

   Then (u, v) = f(x, y) assigns the two return values to local variables u and v, while v = f(x,y) returns a list of two values. Note that in (u, v) = f(x, y) and v = f(x,y), the behavior of v = f(x,y) is not affected by the assignment.

8. Calling function without passing argument value

   Calling f with no argument is done by f(). The empty pair of round brackets is necessary. Without it, the value of the expression f is the function $f$ itself, not a call to the function without argument.

9. max(x) returns the largest element of x no matter x is a vector or a matrix. There are two functions rowmax and columnmax which return the maximums of rows and columns respectively. The same is true for min, sum, mean, etc.

10. There is only one global variable -- but it's more than enough.

    There is only ONE global variable, whose name is global. global itself cannot be assigned to. global is a structure, which may have a bunch of fields. You can modify a field, and can add new fields to it also. For example, you can add a new field format to global

    global.format = "short";
    

    Now global.format can be accessed anywhere. Without the keyword global, format would still refer to the same thing, unless a local variable format has been defined. Functions should usually be declared as global variables if they are intended to be called with other functions.

11. Function Parameters

    Function definitions can carry parameters so that they can be customized later. For example, function $f(x) = \sqrt{x^2+\alpha^2}$ can be defined as

    f = function [alpha = 1] x -> y
              y = sqrt(x^2+alpha^2);
        end
    

    where the default value of the parameter is $\alpha=1$. To change the parameter value to 3, do this

    f.alpha = 3;
    

    or make a anoter copy of f with $\alpha=2$ by

    g = f;
    f.alpha = 3;
    

    or

    g = f[3];
    

12. Partial Substitution

    Functions can be called with only part of the argument values given . The outcome of such a function call is a new function. For example, if $f$ is defined by

    f = function (t, a, b, c, d) -> z
           ....
        end
    

    Then $f$ is a function of 5 arguments. The following commands can be used to create a new function out of $f$ that accepts 2 arguments t and y

    g = f(., ., 5, -2, 3);
    

    where b, c, d are given values 5, -2, and 3 respectively.

    New function g behaves completely like a user defined function, and user doesn't need to know that it is not defined directly in a file. If you want to integrate f as a function of t at given values of parameters a, b, c, d, you can do it like

    int(f(., 1, 5, -2, 3), [0, 1]);
    

    The effect is the
    $$\int_0^1 f(t, 1, 5, -2, 3)dt$$
    Partial substitution is an alternative way of using function parameters. However, the parameter approach is more efficient and has the advantage that parameter values can be viewed and modified.

Operators

• Shang provides the c-style operators ++, -, +=, -=, *=, /=.

• The percent sign % is used as the mod operator.

• # is the operator for list indexing: x # 3 is the third element of list x.

• @ is the operator for retrieving a value from a hash table: x @ "fred" is the value in x associated with key "fred".

• in is the operator for testing set membership: x in S is true if x is a member of set S.

• to is the operator for creating an interval: 0 to 10 is the closed interval [0, 10].

Keywords

These are the keywords reserved in Shang language. as, automaton, break, builtin, catch, common, conditional, continue, do, else, elseif, end, function, global, if, in, on, parent, private, public, readonly, return, self, stop, this, to, try, until, while, yield

• function, class, automaton, conditional are used to define functions, classes, etc.

• parent is used to reference a class member in a member attribute functions.

• this appearing in a function definition refers to the function itself.

• public, private, common, auto, readonly are access control types of class member attributes and function parameters.

• stop and yield are used in an automaton.

• try, catch, throw are used in exception handling.

Flow Control

In addition to the normal control structures Matlab has, Shang provides unless-end, until-end, do-while, and and do-until statements. For example

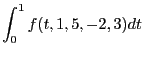
   s = 0;
   k = 1;
   n = 10000;
   do 
      s += 1 / k++;
   while k < n;     // or "until k >= n;"

Plot

Shang is not equipped with built-in functionalities for plotting. A set of programs written in Shang language can create graphics in postscript format. To use it, the program "plot.x" needs to be run first. Here is a simple example

    with("plot.x");
    x = linspace(-pi, pi);
    y = exp(-0.3 * x.^2) .* cos(5 * x);
    z = exp(-0.3 * x.^2) .* sin(5 * x);
    fig = figure.new();
    fig.plot(x, y);
    fig.plot(x, z);
    fig.save("example.eps");

You need a postscript viewer to view, print, or conver the .eps files.

Other data types and constructs

1. Lists

   Shang does not have cell array, but it has a host of data structures in addition to numerical matrices. Among these data structures, lists are arrays whose elements can be anything, including matrices, strings, functions, tables, structures, and objects. Lists might function similarly to the cell arrays of Matlab.

2. Pointer and Pass by reference

   Shang passes function arguments strictly by value. However, by using pointer, it's possible to emulate passing by reference. The following is how the swap function can be implemented

   swap = function (p, q) -> ()
        temp = p>>;  // store in temp the value pointed to by p
        p>> = q>>;   // p now points to the value pointed by q
        q>> = temp;  // q now points to temp
   end
   

   The caller must pass two pointers to the swap function

   >> a = "AAA";
   >> b = "BBB";
   >> swap(>>a, >>b);
   >> a, b
      BBB
      AAA
   end
   

   If you want to alter an argument value, you also have to pass a pointer. For example

   f = function (p, k, x) -> ()
         p>> [k] = x;
   end
   

   Test it

   >> x = zeros(1, 3);
   >> f(>>x, 2, rand(1));
   >> x
      0  0.239  0
   

3. Hash Table

   A hash table is a set of key-value pairs. Each value can be retrieved by providing the associated key. Here is how you can create a hash table, retrieve a value, add key-value pair, and update values:

   >> A = {"red" => "maple", "purple" => "lilac", "grey" => "ash"}
   >> A @ "purple"
      lilac
   >> A @ "violet" = "lavender";
   

   A hash table can also act like a function, therefore in the above A("purple") returns lilac as well.

4. Structure

   A structure is a group of attribute values with each one associated with an identifier. It is very easy to create by using a pair of braces. Each attribute is declared and initialized by assigning the value to the identifier, and all attributes are enclosed in a pair of braces. For example

   >> dims = {length = 15, width = 10, height = 9,
              verify = () -> parent.length * parent.width * parent.heigth <= 1000};
   >> dims.height
      9
   >> dims.height = 12
   >> dims.height
      12
   

   Note that since function is also a data type, attributes of a structure can be functions as well. For example

   >> dims = {length = 15, width = 10, height = 9,
              verify = () -> parent.length * parent.width * parent.height <= 1000};
   >> dims.verify()
      0
   

5. Stack and Queue

Set

The expression

    x in S

or

    x (- S

tests if a value x belongs to a set S.

The following are several ways to create sets.

1. Finite set

   Finite sets can be created by listing all the members

   colors = {"red", "orange", "yellow", "green", "blue", "purple"}
   faces = {1, 2, 3, 4, 5, 6}
   

2. Interval

   Intervals of real numbers are created by using the to operator

   I1 = -1 to 1;        // closed interval [-1, 1]
   I2 = -1+ to 1-;      // open interval (-1, 1)
   I3 = (-1 to 1-);      // interval [-1, 1)
   I4 = (-1+ to inf);     // (1, infinity)
   

3. Sets Defined by Functions

   Any function can be used as a set. If the logical value of f(x) is true, then x is considered a member of set f. For example

   S = x -> (x <= 0 || x >= 1);
   

   There are many built-in sets (or built-in functions), for example, _R is the set of all real numbers, _R2 is the set of all vectors of real numbers of length 2, etc.

4. Sets created by set operations

   Union operator \/, intersection operator /\, and set difference operator \ can be used to create new sets from existing ones.

5. Class as set

   A class is considered the set of all its members, and hence naturally can be be used as a set.

Class and Members

Shang has full support for object oriented programming. In addition to most of the standard ingredients of OOP, several inovative features including member attribute domain, validator, and conditional class make the class interface cleaner, more expressive, and OOP both safer and more flexible. The following demonstrates how simple classes can be created and how domains are used. For more details refer to the language reference manual.

// create a circle class. Note that a class is, like a function, a value, and
// therefore should be assigned to a variable. So "circle" is not the name of
// the class, but the name of the variable used to store the class
circle = class 
              public radius = (0+ to inf);
              auto   perimeter = () -> 2 * pi * parent.radius;
              auto   area = () -> pi * (parent.radius)^2;
         end
person = class
           public gender = "M" in {"F", "M"};
           public age = 1 in (1 : 150);
           public firstname = "Mark" in ~/[A-Za-z][A-Za-z]*/;
           public lastname = "Brown" in ~/[A-Za-z][A-Za-z]*/;
         end

Numerical data types

1. Integer

   The size of an integer depends the int type of the C compiler. Usually an integer uses 32 bytes of memory and has a value between -2147483647 and 2147483647.

   An integer constant is entered with the z suffix. For example, 2899z is an integer while 2899 is a double precision number.

   If all the elements in a bracket expression are integers, the result is an integer matrix. For example, [2z, -3z, 56z].

   The set of all integers is _Z.

2. Arbitrary precision floating point number

   A number with suffix M is an Mpf constant.

      >> x = 1.3352M
         1.33519999999999999999999999999999E0
   

   Operations involving Mpf usually produces Mpf results. » sqrt(x) 1.15550854605234313688808503023426E0

   An Mpf matrix is created if all components in a bracket expression are Mpf's

      >> X = [3.1M; 2.2M; -1.55M]
   
         3.09999999999999999999999999999999E0  
         2.19999999999999999999999999999999E0  
         -1.54999999999999999999999999999999E0
   

   The functions zeros, ones, and rand returns Mpf matrices if the last argument is _M. For example

      >> x = rand(5, 1, \_M)
      9.3021775040240436056832347452058E-1  
      8.5311813443668253119942506400455E-1  
      7.7238437656903267296393271625706E-1  
      5.8162992980263383743533686828037E-1  
      8.8838553079998591821584992499428E-1
   

   The following commands solve a system of linear equations using Mpf

      >> A = rand(10, 10, \_M);
      >> b = rand(10, \_M);
      >> x = A \ b;
      >> norm(A * x - b)
         4.7817994155912976409669674814276E-38
   

   The default precision of Mpf is 128 binary digits, or about 38 decimal digits. The precision can be changed by assigning a new value to global variable mpf_ndigits. The new value must be a multiple of 32.

      >> global.mpf\_ndigits = 256;
      >> r = sqrt(2M);
      >> r\^2 - 2M
         -3.45446742203777785e-77
   

   Note that Mpf computations are much much slower and more resource consuming than regular double precision computations.

3. Long integer

   A number with suffix L is a long integer. The magnitude of a long integer is limited only by the system's resources. For example

      >> n = 123456789012345678901234567890L
         123456789012345678901234567890
      >> factorial(50L)
         30414093201713378043612608166064768844377641568960512000000000000
   

   Be very careful when using long integers, one integer that is too long may use up all the system memory.

4. Byte

   A byte is a small integer with value between 0 and 256. A byte is entered with B suffix, like 35B. A matrix of bytes is created with domain specified by the set _B. For example, x = zeros(15, _B);

About this document ...

A Quick Guide to Shang for Matlab Users

This document was generated using the LaTeX2HTML translator Version 2002-2-1 (1.71)

Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999, Ross Moore, Mathematics Department, Macquarie University, Sydney.

The command line arguments were:
latex2html -split 0 formatlabusers.tex

The translation was initiated by on 2012-01-12