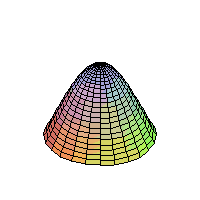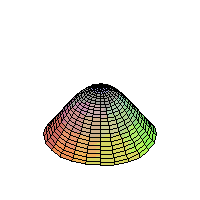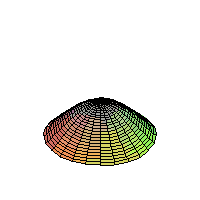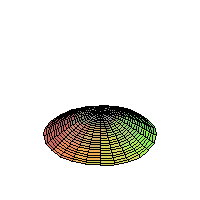
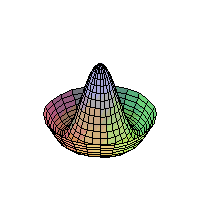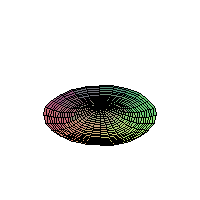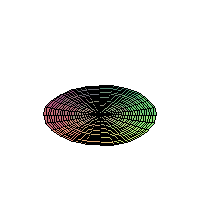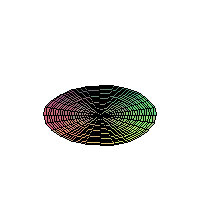
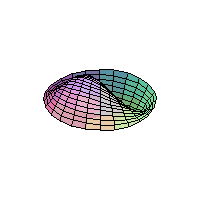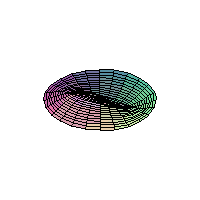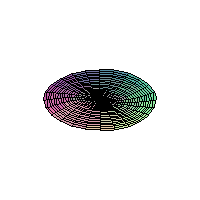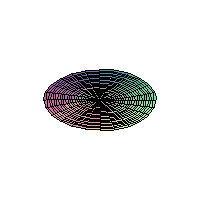
The 2D Heat Equation on a Disk;

Homogeneous Dirichlet Boundary Conditions

$exp(-k$0,12 t) J0(k0,1 r) $k$0,1 = 2.404825558...	$exp(-k$0,22 t) J0(k0,2 r) $k$0,2 = 5.520078110...	$exp(-k$0,32 t) J0(k0,3 r) $k$0,3 = 8.653727913...
$exp(-k$1,12 t) J1(k1,1 r) cos(θ) $k$1,1 = 3.831705970...	$exp(-k$1,22 t) J1(k1,2 r) cos(θ) $k$1,2 = 7.015586670...	$exp(-k$1,32 t) J1(k1,3 r) cos(θ) $k$1,3 = 10.17346814...
$exp(-k$2,12 t) J2(k2,1 r) cos(2θ) $k$2,1 = 5.135622302...	$exp(-k$2,22 t) J2(k2,2 r) cos(2θ) $k$2,2 = 8.417244140...	$exp(-k$2,32 t) J2(k2,3 r) cos(2θ) $k$2,3 = 11.61984117...
$exp(-k$3,12 t) J3(k3,1 r) cos(3θ) $k$3,1 = 6.380161896...	$exp(-k$3,22 t) J3(k3,2 r) cos(3θ) $k$3,2 = 9.761023130...	$exp(-k$3,32 t) J3(k3,3 r) cos(3θ) $k$3,3 = 13.01520072...

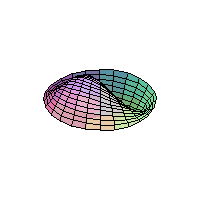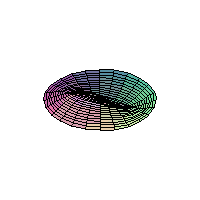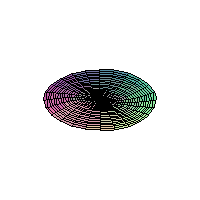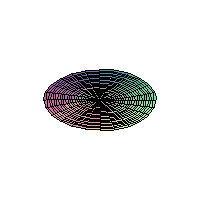
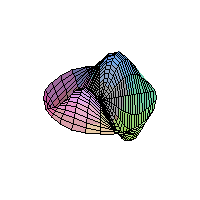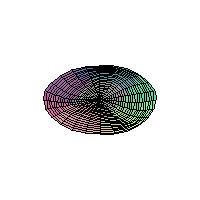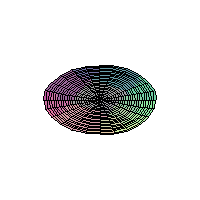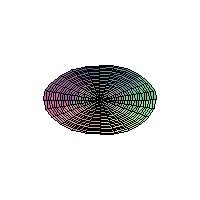
These animations were generated using Waterloo MAPLE, and were optimized using the GIMP image manipulation program.

Return to Math 305 Animations Page