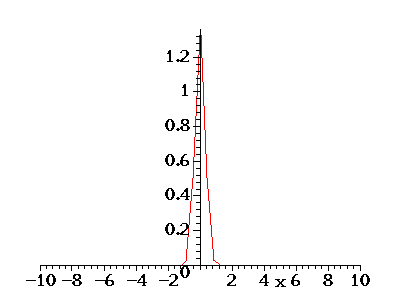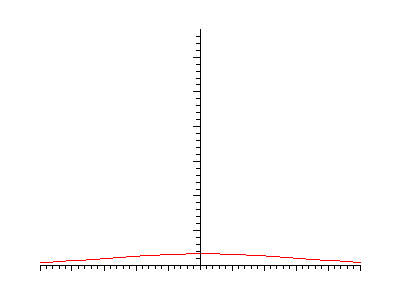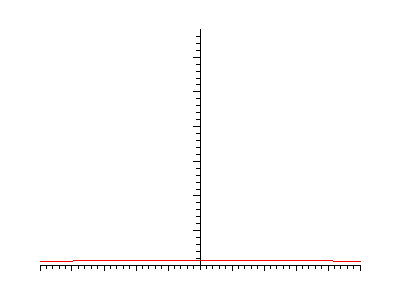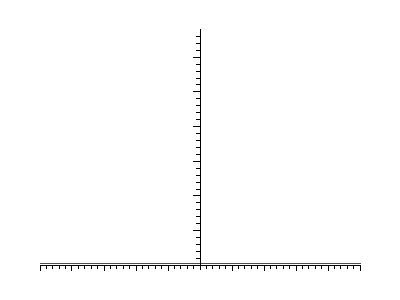
The Gauss-Weierstrass Kernel
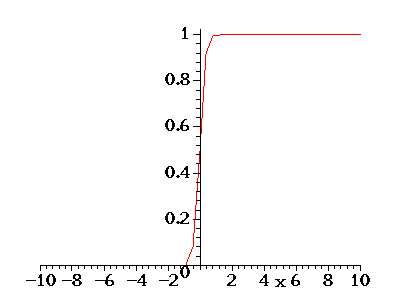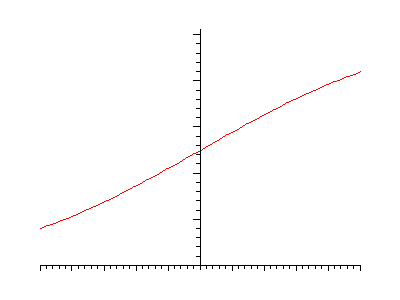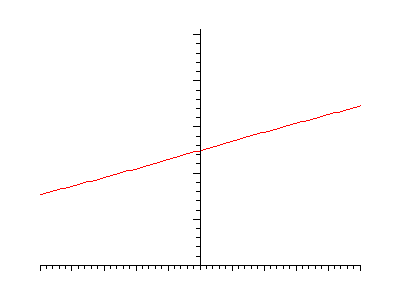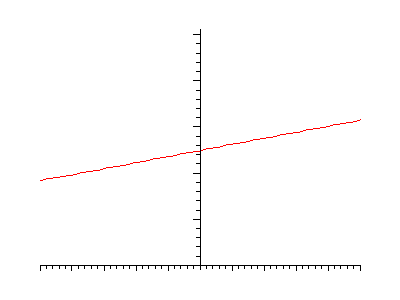
Initial conditions: Heaviside step function:
Solution by Gaussian Convolution:
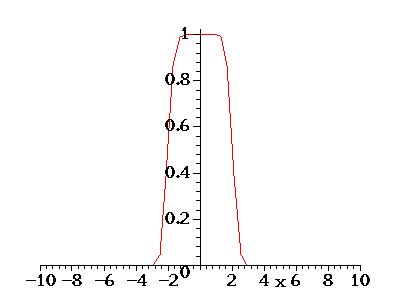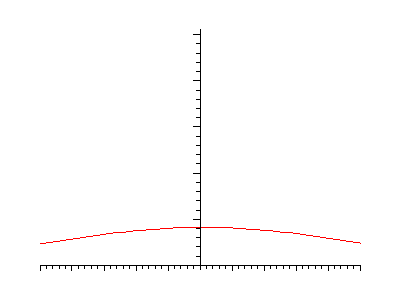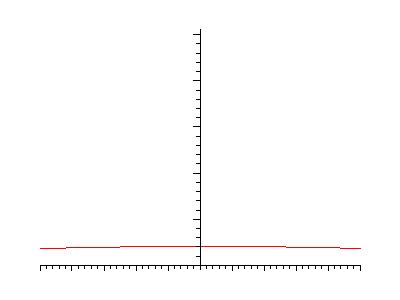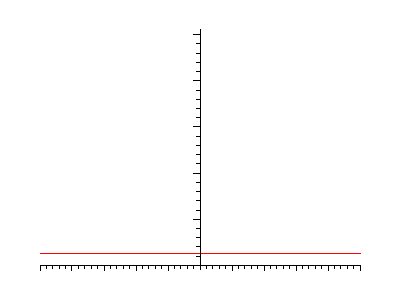
Initial conditions:
Solution by Gaussian Convolution:
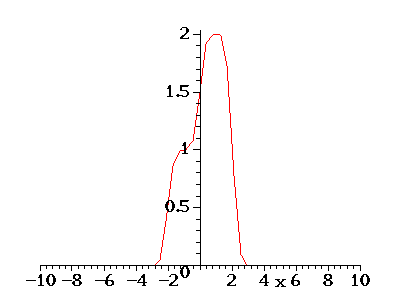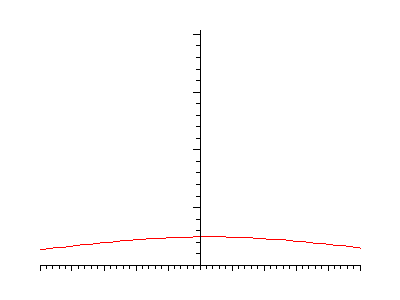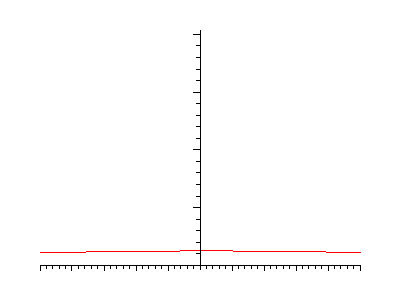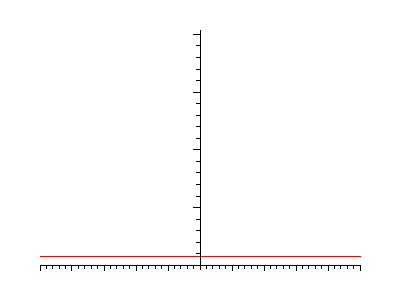
Initial conditions:
Solution by Gaussian Convolution:
The 1D Heat Equation on the Real Line
The Gauss-Weierstrass Kernel

The Gauss-Weierstrass Kernel |

Initial conditions: Heaviside step function: Solution by Gaussian Convolution: |

Initial conditions: Solution by Gaussian Convolution: |

Initial conditions: Solution by Gaussian Convolution: |
These animations were generated using Waterloo
MAPLE, and were optimized using the
GIMP image manipulation
program.
Return to Math 305 Animations Page