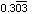Mathematics 280


Test 1
1997

TIME: 90 minutes

  1. Find the greatest common factor and least common multiple of 24, 100 and108. [4 marks]

  2. Write the repeating decimal as a rational number in lowestterms. [3 marks]

  3. (a) Show that the ISBN 0-201-11958-4 is not correct.
    (b) If it is known that the only incorrect digit is the "8" in the next-to-last position,find the correct ISBN. [4 marks]

  4. The following diagram represents the floor plan of a house with 5 roomsand 7 connecting doors. We want to know if it is possible to take a walkthrough this house, passing through every door exactly once.

    (a) Draw a graph that can be used to analyze this problem. Clearly indicatewhat the vertices and edges represent.
    (b) Which "graph concept" corresponds to the problem that has been posed? Using graph terminology, answer thequestion. If it is possible to take a walk passing through every door exactlyonce, show how; if it is impossible, explain why.
    (c) Answer the samequestion with the added restriction that the walk must end where it begins. Ifit is possible to take such a walk, show how; if it is impossible, explain whyand find the minimum number of doors that must be passed through twice in orderto accomplish this and show how. [6 marks]

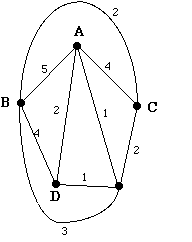
  5. (a) Using Kruskal'sAlgorithm, find a minimum-cost spanning tree for the graph shownbelow. Clearly indicate the order in which the edges are chosen.

    (b) Usingthe nearest neighbour method starting at A, find an approximate solution to theTravelling Salesperson's Problem for this graph. Is this the optimal solution? [4 marks]

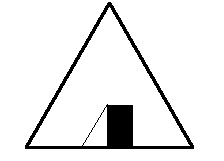
  6. (a) Show how the pattern below would be extended by a 60-60-60 kaleidoscope if the heavy linesrepresent the mirrors. (Draw enough of the pattern so that the undrawn portionsimply consists of translations of the portion you have drawn.)

    (b) Showhow the pattern can be used to explain the effect of doing (1) two reflectionsin intersecting mirrors, and (2) two reflections in parallel mirrors. [4 marks]

Back to the Math 280 home pageBackto MathBack to the Math home page