Assignment #3
Due: 2 November, 1998
Getting a squash court
When the athletic centre at Unseen University opens at 8 a.m., people start to line up to book squash courts for the following day. At 8:10 the sign-up sheet is brought out and the line starts to move at the rate of six people per minute; that is, it takes each player ten seconds sign up for a court. Below is a graph of the total number n of people who have arrived to sign up for a court by t minutes past 8 a.m.
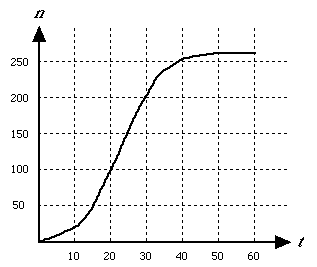
For example, the height of the graph at t = 30 is n = 200, which means that the 200th person arrives at 8:30.
Use the graph to answer the following six questions.
- How many people are in the line-up at 8:30? [1]
- At what time does the line-up disappear? [2]
- Hint: The people in line at any given time are those who have arrived but have not yet signed up. The "arrival" graph above should be combined with a "departure" graph of the total number of people who have signed up by time t.
- At what time is the line-up longest? [2]
- How long does the 120th person to arrive have to stand in line?[1]
- When does the person who will have to stand in line longest arrive? [2]
- Suppose there are 120 prime slots and that these go to the first 120 people to arrive. At what time should you arrive if if you want to get a prime slot, but spend as little time as possible in line? [2]
Bonus. What city is Unseen University in? [0.2]
Department of Mathematics
Trent University
Maintained by Stefan Bilaniuk. Last updated 1999.12.03.