![[diagram]](illumination.gif)
1. A level surface is illuminated by a single lamp. The intensity of illumination of a small piece of the surface is directly proportional to the cosine of the angle of incidence of the light and is inversely proportional to the square of the distance from the light source. If we draw a circle 10 m wide on the surface, how high above the centre of the circle must we place the lamp to maximize the intensity of illumination at the edge of the circle?
Solution. Let us label various of the quantities involved as in the diagram
![[diagram]](illumination.gif)
and denote the intensity of illumination at the edge of the circle by I. From what we are told about what intensity of illumination is proportional to, it follows that
 ) / s2,
) / s2,
where C is some constant. The precise value of C depends on the intensity of the light source and the choice of units in which to measure intensity. We will assume C is positive -- as it turns out to be for most reasonable choices of units -- in what follows.
The basic idea is to rewrite our equation for I in terms of h and apply our max/min technology. Note that cos( ) = I/s and, by Pythagoras, s2 = h2 + 52, so s = (h2 + 25)1/2. It follows that
) = I/s and, by Pythagoras, s2 = h2 + 52, so s = (h2 + 25)1/2. It follows that
Note that because h2 + 25 is never 0, I is defined for all h. It should be clear from the set-up, however, that h must be at least 0.
Differentiating I with respect to h using the Quotient Rule gives
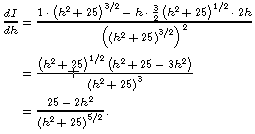
Thus I' = 0 exactly when 25 - 2h2 = 0, i.e. when h = +- (25/2)1/2 = +- 5/21/2. Since we know that h is non-negative, we only have to consider the critical point h = 5/21/2.
To find the maximum for I we now have to compare its values at the endpoints of the range of possible h's with its value at the critical point:
Thus the maximum intensity of illumination at the edge of the circle is achieved when the light source is 5/21/2 (about 3.53553) metres above the centre of the circle.
2. A two-player game (in which the players take turns making moves) is considered to be finite if it cannot go on forever when played by the rules. The two-player game SUPERGAME is played as follows: the first player chooses a finite two-player game, which the two players proceed to play out with the second player going first. Is SUPERGAME itself finite? Why or why not?
Solution. SUPERGAME cannot itself be a finite game because a contradiction would arise if it were:
Suppose SUPERGAME were a finite game. Then choosing SUPERGAME would be a valid first move in a game of SUPERGAME. But then a legal game of SUPERGAME could go on forever: the first player makes the first move and chooses SUPERGAME as the finite game to be played out. Now the second player has to make the first move in a game of SUPERGAME, and chooses SUPERGAME too. This leaves the first player to make the first move in a game of SUPERGAME, who chooses SUPERGAME again, which leaves the second player to make the the first move in a game of SUPERGAME, who...The fundamental problem here is that the notion of "finite two-player game", in terms of which SUPERGAME was defined, was not really precise. (Heck, the notion of "game" was never precisely defined here. How would you do that?) To avoid the contradiction above, any attempt to make the notion of "finite two-player game" really precise would have to have to be sufficiently restrictive to exclude SUPERGAME.
 Department of Mathematics
Department of Mathematics
 Trent University
Trent University