![[diagram]](balloon2.gif)
 cm long lies as straight as possible on the surface of a spherical balloon while it is being inflated. The balloon remains spherical at all times, and the hair, which doesn't stretch or shrink, remains as straight as possible on its surface.
cm long lies as straight as possible on the surface of a spherical balloon while it is being inflated. The balloon remains spherical at all times, and the hair, which doesn't stretch or shrink, remains as straight as possible on its surface.
Solution. The key to understanding this set-up is that it is really only two-dimensional. If you were to cut the balloon --- imagine that it wouldn't just pop! --- along the hair, you would cut right through the center of the balloon. A diagram of the resulting cross-section, with various lines and angles drawn in and labelled, is given below. Note that the cross-section is just a circle with the same radius as the balloon.
![[diagram]](balloon2.gif)
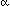 radians --- that is, the length of the hair --- is just r
radians --- that is, the length of the hair --- is just r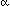 . (This simplicity is one of the pleasant benefits of using radians.) In our set-up, this means that
. (This simplicity is one of the pleasant benefits of using radians.) In our set-up, this means that
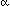 = 2
= 2 .
.
This also lets us determine the angle 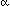 at the instant when = 4: if 4
at the instant when = 4: if 4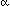 = 2
= 2 , then
, then 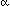 =
=  /2.
/2.
Second, the length c of the chord corresponding to the arc subtended by 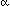 --- that is, the distance between the ends of the hair --- can be computed from one the symmetric right triangles in the diagram, to get c/2 = rsin(
--- that is, the distance between the ends of the hair --- can be computed from one the symmetric right triangles in the diagram, to get c/2 = rsin(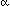 /2). Thus
/2). Thus
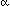 /2),
/2),
and, at the instant when = 4 and 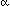 =
=  /2, c = 8sin(
/2, c = 8sin( /4) = 4
/4) = 4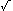 2.
2.
Third, the distance a between the midpoint of the hair and the chord --- that is, line between the two ends of the hair --- can be obtained by subtracting the radius of the balloon from the height of the triangle whose base is the chord and whose tip is the centre of the balloon. Using one the symmetric right triangles again gives us r2 = h2 + (c/2)2, so h = 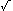 (r2 - c2/4). Thus
(r2 - c2/4). Thus
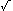 (r2 - c2/4).
(r2 - c2/4).
a. How is the radius of the balloon changing when it is 4 cm, if the ends of the hair are moving apart at 1 cm/s at that instant?
We are told that c' = 1 and need to find r'. Since r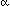 = 2
= 2 , we have that
, we have that 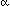 = 2
= 2 /r. So we can express c in terms of r alone,
/r. So we can express c in terms of r alone,
 /2r) = rsin(
/2r) = rsin( /2r),
/2r),
and differentiate away with respect to c on both sides:
![[calculation]](S3-calc1.gif)
Since r = 4 at the instant in question, this gives
![[calculation]](S3-calc2.gif)
It follows that the radius is changing at a rate of
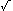 2 / (4 -
2 / (4 -  ) .
) .
That amounts to roughly 3.3. Thus, at the instant in question, the radius of the balloon is growing --- note that r' is positive! --- at a rate of about 3.3 cm/s.
b. At the same instant, how quickly is the midpoint of the hair aproaching the line between the two ends?
We know r' at this instant from part a, and we are given c', so all we have to do is differentiate away in
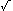 (r2 - c2/4) .
(r2 - c2/4) .
Then
![[calculation]](S3-calc3.gif)
so, at the instant in question,
![[calculation]](S3-calc4.gif)
That amounts to roughly -0.9. This means that the middle of the hair is getting closer --- note the sign! --- to the line joining the ends at a speed of about 0.9 cm/s. Q.E.D.
2. Suppose that two squares are cut off diagonally opposite corners of a standard 8  8 chessboard. If you are given 31 dominoes, each of which is just the right size to cover two adjacent squares of the board, can you place them so that all 62 remaining squares of the board are covered? You should either show how this can be done or prove that it cannot be done.
8 chessboard. If you are given 31 dominoes, each of which is just the right size to cover two adjacent squares of the board, can you place them so that all 62 remaining squares of the board are covered? You should either show how this can be done or prove that it cannot be done.
Solution. It can't be done. To see why not, observe that every domino must cover a square of each colour, one black and one white. Thus 31 dominoes covering 62 squares must cover 31 white squares and 31 black squares. However, the mutilated board has 30 of one and 32 of the other... Q.E.D.
 Department of Mathematics
Department of Mathematics
 Trent University
Trent University