 (x) by
(x) by 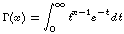 .
.
a. Verify that this definition makes sense whenever x > 0. [3]
b. Show that  (x)(1) = 1 and that
(x)(1) = 1 and that  (x+1) = x
(x+1) = x (x) whenever x > 0. [3]
(x) whenever x > 0. [3]
c. If n is a positive integer, what is  (n)? [1]
(n)? [1]
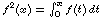 . [3]
. [3]
 (x) by
(x) by 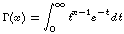 .
.
b. Show that  (x)(1) = 1 and that
(x)(1) = 1 and that  (x+1) = x
(x+1) = x (x) whenever x > 0. [3]
(x) whenever x > 0. [3]
c. If n is a positive integer, what is  (n)? [1]
(n)? [1]
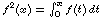 . [3]
. [3]
 Department of Mathematics
Department of Mathematics
 Trent University
Trent University